ボイルシャルルの法則の計算例題を集めました。
解答には公式もありますのでチェックしてみてください。
それではさっそく参りましょう、ラインナップは目次からどうぞ 🙂
目次
ボイルシャルルの法則や理想気体の例題（熱力学）公式付き
【例題】
一定体積V=2.0㎥の容器に圧力p₁=0.5MPa、温度t₁=20℃の空気が入っており、圧力をP₂=1MPaにまで上昇させたい。
ただし、空気の定容比熱Cv=0.7kJ/(kg・K）、ガス定数R=287J/(kg・K）とする。このとき、次の問いに答えなさい。
(1)空気の質量mはいくらか。
(2)空気の温度T₂は何【K】になるか。
(3)このとき加えるべき熱量Qはいくらか。
一方、熱力学の法則には第一法則、第二法則がありますので、併せてチェックしてみてください。
【問題】ボイル・シャルルの法則！計算例題＆解答まとめ
問題はこちら 🙂
①ボイルの法則1
1.0atmで20ℓの気体を、温度一定で圧力を2.5atmにすると体積はいくらか。
②ボイルの法則2
断面積がSで質量の無視できるなめらかなピストンをもつシリンダーがあり、中には体積V₁の理想気体が入っている。シリンダー外部の大気圧はP₀であった。
以下の問いに答えなさい。
(1)シリンダー内の気体の圧力P₁を求めよ。
(2)ピストンの上に質量Mの重りをのせるとき、シリンダー内の気体の圧力P₂と、体積V₂はいくらになるか。ただし、シリンダー内の温度は外部と同じ温度とする。
③1.ボイルシャルルの法則
0℃、1.0atm、20ℓの気体を、273℃、3.0atmにすると、体積は何ℓになるか。
④2.ボイルシャルルの法則
容積240㎥の部屋があり、室内の温度は0℃、圧力は1atmであった。
1atmのまま、この室内の空気の温度を17℃に上げると、何㎥の空気が部屋から出ていくか。
⑤3.ボイルシャルルの法則（応用）
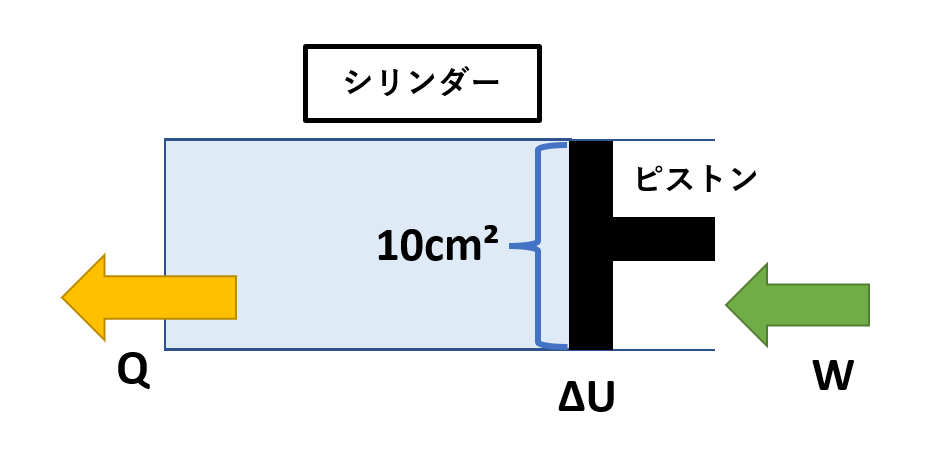
上記図解のように、なめらかに動くピストンをもつシリンダ内に27℃、0.3ℓの気体が入っている。大気圧は1.0×10⁵Pa、ピストンの断面積は10cm²であった。
いま、気体の状態変化で、気体が外部にする仕事をW、外部からもらう熱量をQ、気体の内部エネルギー変化をΔUで表すこととする。
このとき、A、Bそれぞれの問いに答えなさい。
【A】まず気体の温度を127℃にした。
(1)気体の体積を求めよ。
(2)ピストンが外部にした仕事Wを求めよ。
(3)気体の内部エネルギー変化ΔUをQやWを使って表せ。
【B】温度27℃、0.3ℓの状態でピストンを固定し、その後気体の温度を127℃にした。
(4)気体の圧力を求めよ。
(5)気体が外部する仕事Wを求めよ。
(6)気体の内部エネルギー変化ΔUをQやWを使って表せ。
【解答】ボイルシャルルの法則！計算例題＆解答まとめ
解答をみていきましょう。（確認のため公式も記載しておきます）
【ボイル・シャルルの法則★公式】
| ボイルの法則 | 一定温度で、一定量の気体の 体積Vは圧力Pに反比例 | P₁V₁=P₂V₂=k（一定）
V=k/P、PV=k |
| シャルルの法則 | 一定圧力で、一定量の気体の体積Vは絶対温度Tに比例 | V=k’T（k’=0℃の体積/273）
V₁/V₂=T₁/T₂ |
| ボイル・シャルルの法則 | 一定量の気体の体積Vは 圧力Pに反比例し、絶対温度Tに比例 | P₁V₁/T₁=P₂V₂/T₂ |
①ボイルの法則1
1.0atmで20ℓの気体を、温度一定で圧力を2.5atmにすると体積はいくらか。
【解答】
ボイルの法則により、
1.0×20=2.5V
V=8.0ℓ
解答：体積8.0ℓ
②ボイルの法則2
断面積がSで質量の無視できるなめらかなピストンをもつシリンダーがあり、中には体積V₁の理想気体が入っている。シリンダー外部の大気圧はP₀であった。
以下の問いに答えなさい。
(1)シリンダー内の気体の圧力P₁を求めよ。
(2)ピストンの上に質量Mの重りをのせるとき、シリンダー内の気体の圧力P₂と、体積V₂はいくらになるか。ただし、シリンダー内の温度は外部と同じ温度とする。
【解答】
(1)ピストンの質量を無視すると、P₁=P₀となる。
(2)P₂=P₀+Mg/Sであるから、ボイルの法則により、
P₀V₁=P₂V₂
V₂=P₀V₁S/(P₀S+Mg）
解答：(1)P₁=P₀、(2)V₂=P₀V₁S/(P₀S+Mg）
③1.ボイルシャルルの法則
0℃、1.0atm、20ℓの気体を、273℃、3.0atmにすると、体積は何ℓになるか。
【解答】
ボイル・シャルルの法則により、
1.0×20/273=3V/(273+273)
V=13ℓ
解答：V=13ℓ
④2.ボイルシャルルの法則
容積240㎥の部屋があり、室内の温度は0℃、圧力は1atmであった。
1atmのまま、この室内の空気の温度を17℃に上げると、何㎥の空気が部屋から出ていくか。
【解答】
温度を17℃に上げた時、室内の空気の体積がV㎥になるとすると、シャルルの法則より
240/273=V/(17+273)
V=255㎥
解答：V=255㎥
⑤3.ボイルシャルルの法則（応用）
なめらかに動くピストンをもつシリンダ内に27℃、0.3ℓの気体が入っている。大気圧は1.0×10⁵Pa、ピストンの断面積は10cm²であった。
いま、気体の状態変化で、気体が外部にする仕事をW、外部からもらう熱量をQ、気体の内部エネルギー変化をΔUで表すこととする。
このとき、A、Bそれぞれの問いに答えなさい。
【解答】
【A】まず気体の温度を127℃にした。
(1)気体の体積を求めよ。
ボイル・シャルルの法則より、PV/T=P’V’/T’
圧力Pが等しいので、V/T=V’/T’
シャルルの法則より
V/300=V’/(273+127)
よって、V’=4/3V=4×0.3/3=0.4ℓ
解答：体積0.4ℓ
(2)ピストンが外部にした仕事Wを求めよ。
仕事の式はW=F×Δℓ
ここで、P=F/Sより
W=P×S×Δℓ=PΔV
=1.0×10⁵×(0.4-0.3)×10⁻³
=10J
解答：仕事10J
(3)気体の内部エネルギー変化ΔUをQやWを使って表せ。
解答：ΔU=Q-W
【B】温度27℃、0.3ℓの状態でピストンを固定し、その後気体の温度を127℃にした。
(4)気体の圧力を求めよ。
ボイル・シャルルの法則より、
PV/T=P’V/T’
P/300=P’/400
よって
P’=4/3P=1.33×10⁵Pa
解答：圧力P’=1.33×10⁵Pa
(5)気体が外部する仕事Wを求めよ。
W=PΔV=P×0=0
解答：仕事W=０
(6)気体の内部エネルギー変化ΔUをQやWを使って表せ。
ΔU=Q-W=Q-0
よってΔU=Q
解答：内部エネルギー変化ΔU=Q
以上です。
ありがとうございました。