ラーメン構造の計算例題や特徴について！モーメント図も解説

ラーメン構造の”ラーメン”は、あの美味しいラーメン🍜じゃないんです（笑）

語源の由来はドイツ語の「Rahmen（枠や縁の意味）」からきています。

そんなわけで今回のテーマは【ラーメン構造】

計算例題や特徴、モーメント図についてサクッとみていきましょう。

ラーメン構造の計算例題や特徴について！モーメント図も解説

ラーメン構造の計算とモーメント図についてかんたんに解説します。

計算手順としてはこんな感じです。

断面力は自由体図を描いてつり合い式を立てますが、ラーメン構造になると自由体図の数が増えて計算がむずかしくなります。

自由体図を描き分けるポイントは、

①切断する部材の前後に外力があるか

②柱梁接合部などの部材の折れ曲がりがあるか

で決まりますのでチェックしてみてください。

また曲げモーメント図は荷重の位置に応じたパターン分けができます。

あらかじめ曲げモーメント図の形がイメージできていれば、すぐに計算の間違いにも気づけるので、典型的なものは頭に入れておくと良いですね 😀

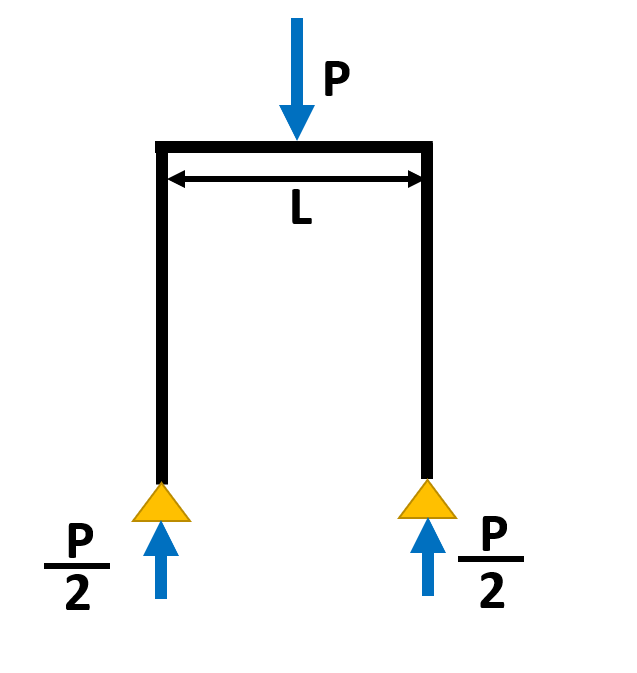
そして計算例題は以下の表をご覧ください。

ラーメン構造例 ＆ モーメント図	計算例
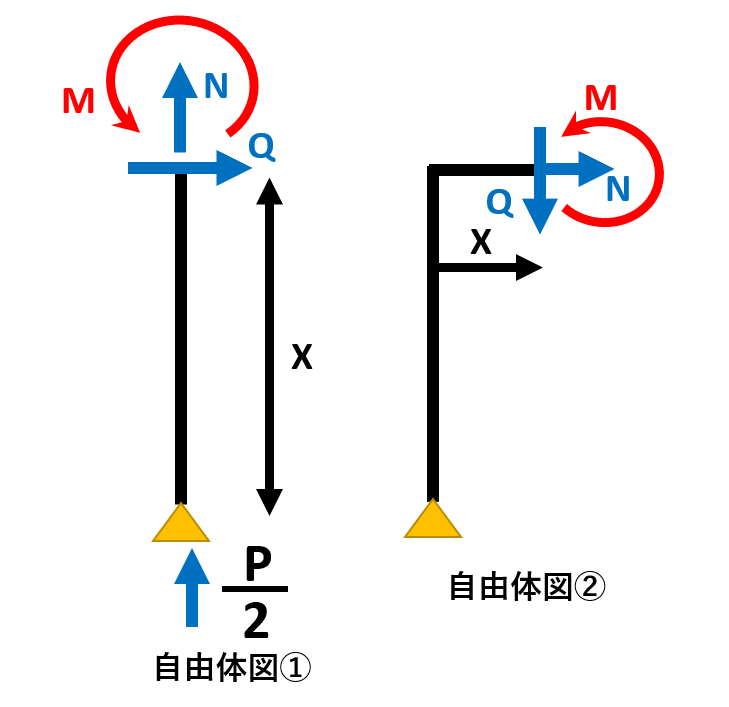
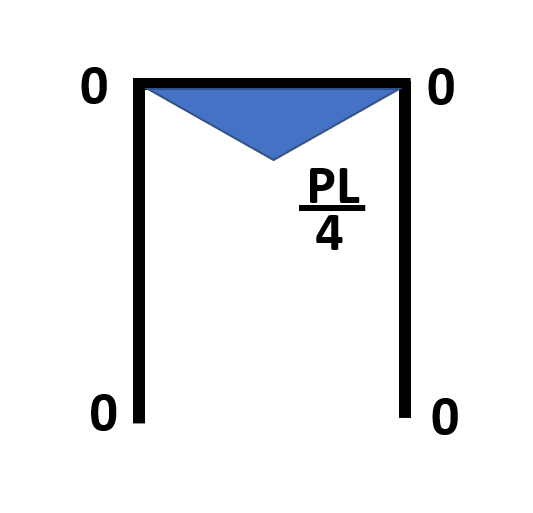
ラーメン構造 モーメント図	N+P/2=0⇒N=-P/2 Q=0 M=0 梁の部分の描き方は、自由体図としてはLを反転させたような形で描き、計算で使う任意の長さ xの位置を梁の端からスタートさせるというのがポイント 任意の長さxは支点からとってもいいけど、計算が難しくなりミスしやすいので梁の端からスタートさせたほうが良い 断面力の向きが再び90°回転することにも注意が必要 この問題の断面力は、つり合い式より、 N=0 Q-P/2=0⇒Q=P/2 M-P/2×x=0⇒M=Px/2 となり、x=L/2のとき、M=PL/4である
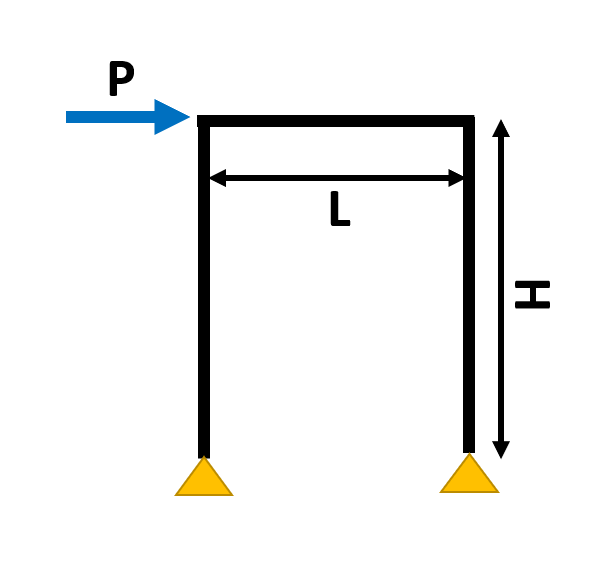
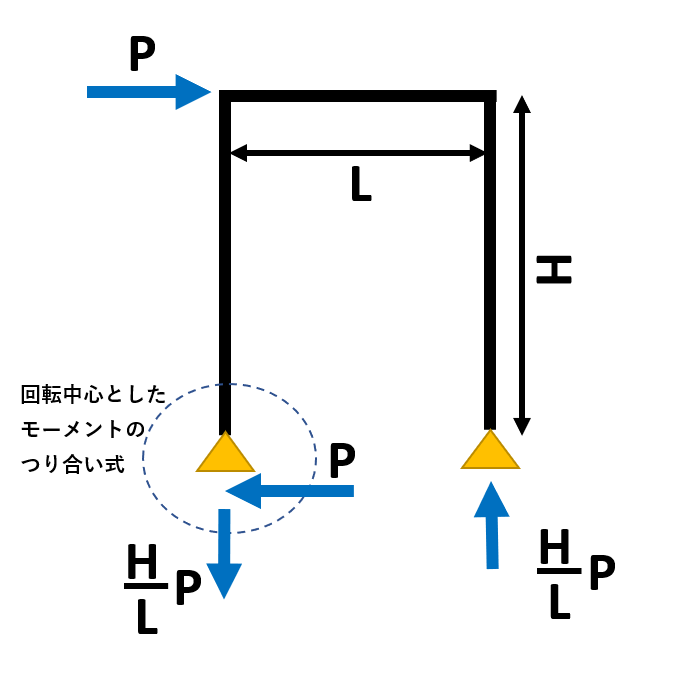
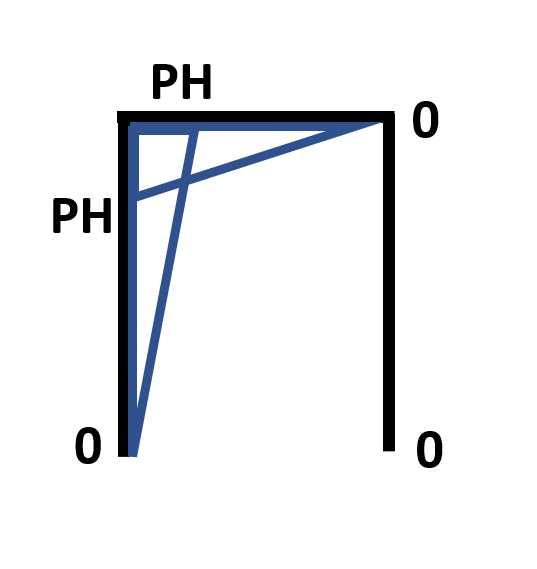
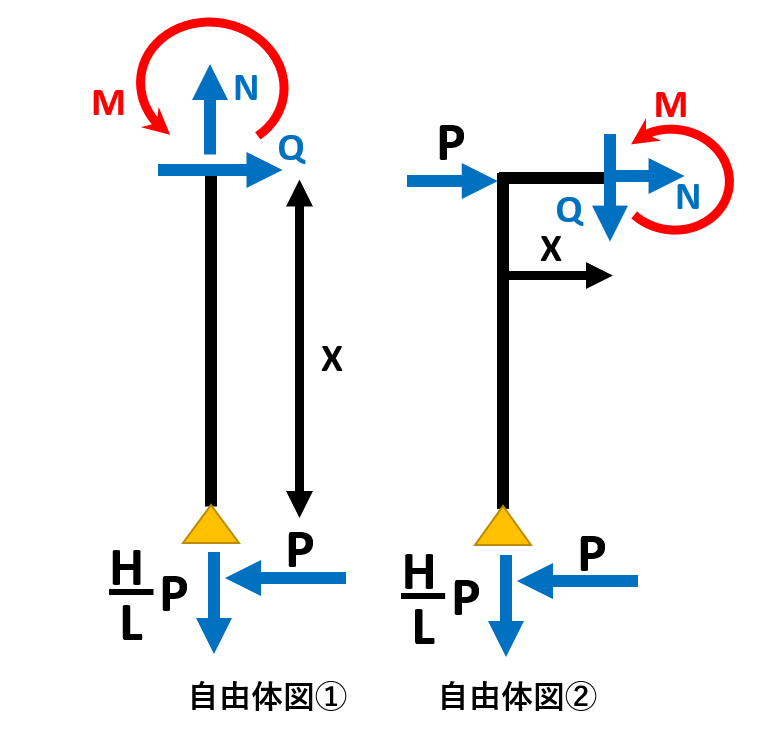
ラーメン構造 モーメント図	それぞれつり合いの式を立てる N=HP/L、M=Px、Q=P 柱頭の位置での曲げモーメントはM=PH N+P-P=0、M-PH+HPx/L=0⇒M=PH-PHx/L

それぞれの部材について分けて考え、また力が0になる部分を見つけるのがポイントです。

ラーメン構造の特徴（メリット＆デメリット）

ラーメン構造の特徴はこんな感じ 🙂

ラーメン構造のメリットは、空間が広い、開口が自由に開けられることです。

ちなみにラーメン構造は建築や土木で最も普及している構造形式と言えるでしょう。

施工、加工が難しくないので工事がスムーズに進みます。

さらに構造設計もカンタンで、他の構造と比べて、検討項目も少なく済みます。

一方で、デメリットは構造的なものがあります。

たとえばブレース構造と比較すると、ラーメン構造のほうが部材が大きくなってしまいます。

これは地震時に作用する曲げモーメントの影響で、対するブレース構造は、地震力をブレースが負担するので、曲げモーメントはほとんど生じません。

よってラーメン構造では、所定の耐力を満たすため柱や梁を大きくしなければなりません。

構造部材が大きいと、構造部材の費用が高くなる可能性も出てくるでしょう。（※全体の費用としては安いまたは同等になる場合もあります）

ラーメン構造の計算例題＆モーメント図まとめ

一般的なラーメン構造のモーメント図は覚えておくと計算での間違いに気づきやすい

以上です。

ありがとうございました。