アローダイヤグラム法とは、矢印と結合線を用いた図で表し、効率的な日程計画作成と進捗を管理する手法です。
計画の段階で、平行作業や前後作業の確認や日程にもっとも時間がかかるルート（クリティカルパス）などを把握できます。
さらに、目標達成のための計画調整にも活用できるのがメリットです。
この記事ではアローダイヤグラム法の書き方や、例題もふくめた解き方などを解説しています。
それではさっそく参りましょう、ラインナップはこちらです。
目次
アローダイヤグラムの書き方！わかりやすく解説
まずはアローダイアグラムの書き方をみていきます。
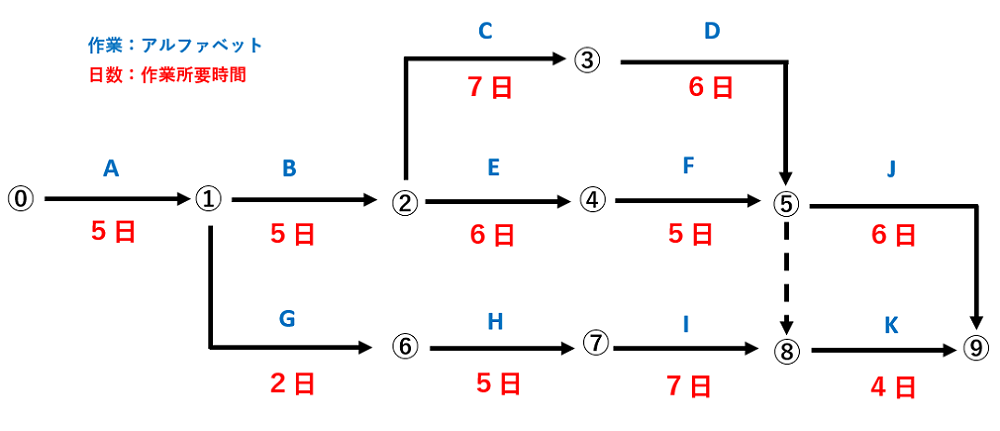
図1アローダイヤグラム概念図
アローダイヤグラムで使う用語と見方は以下の表のとおりです。
矢印（実線・破線）や数字を使って、作業の流れを表します。
| 作業（→） | 作業の進捗。矢印線（→）で示し、作業の開始から終わりを表している。
作業の開始→作業の終わり 作業所要時間や作業名の表現方法 |
| 結合点（○） | 各作業の結合点のこと。
表し方：⓪→① 番号は作業の流れる順に大きくなる。（作業はじめの番号＜作業終わりの番号） 番号は同じ番号が２つ以上あってはならない。 |
| ダミー（‐‐‐‐>） | ダミーとは作業とはちがい、所要時間ゼロの擬似作業のこと
作業の相互関係を表すためにのみ使われる ダミーは破線の矢印で表す‐‐‐‐> |
たとえば、上記（図1）のアローダイヤグラム図では、次のことが読み取れます。
作業②③④は、作業①が終わらなければ始められない
作業④は作業①②③が終わらなければ始められない
アローダイヤグラムの解き方をわかりやすく！例題➀用語や表をえらぶ問題
アローダイヤグラム法を使う問題は、さまざまな資格試験で出題されています。
たとえば、
品質管理検定（QC検定）：用語や表をえらぶ問題
土木施工管理技士の試験：ネットワーク工程表
などがあります。
さっそく例題を見ていきましょう。
アローダイアグラムの例題
【問題】次の文章①～④において、もっとも適切な手法名称とそれを表した概略図を下の選択肢からひとつえらべ。ただし各選択肢は複数回用いることはない。
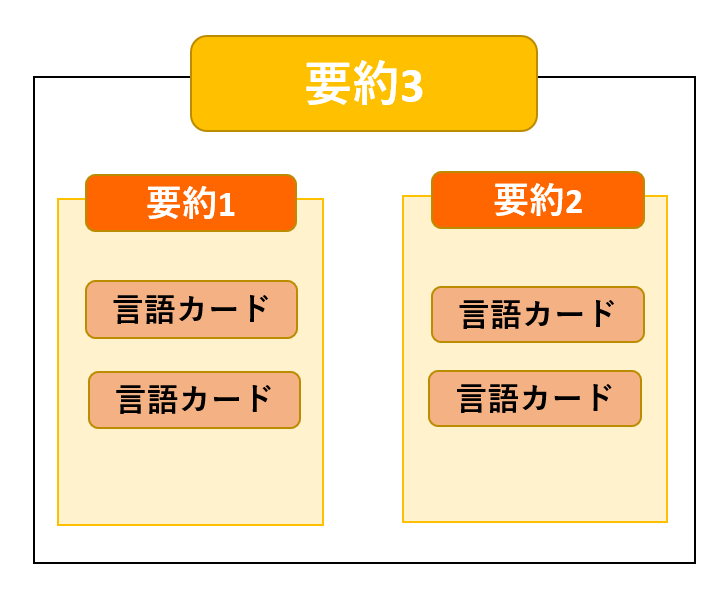
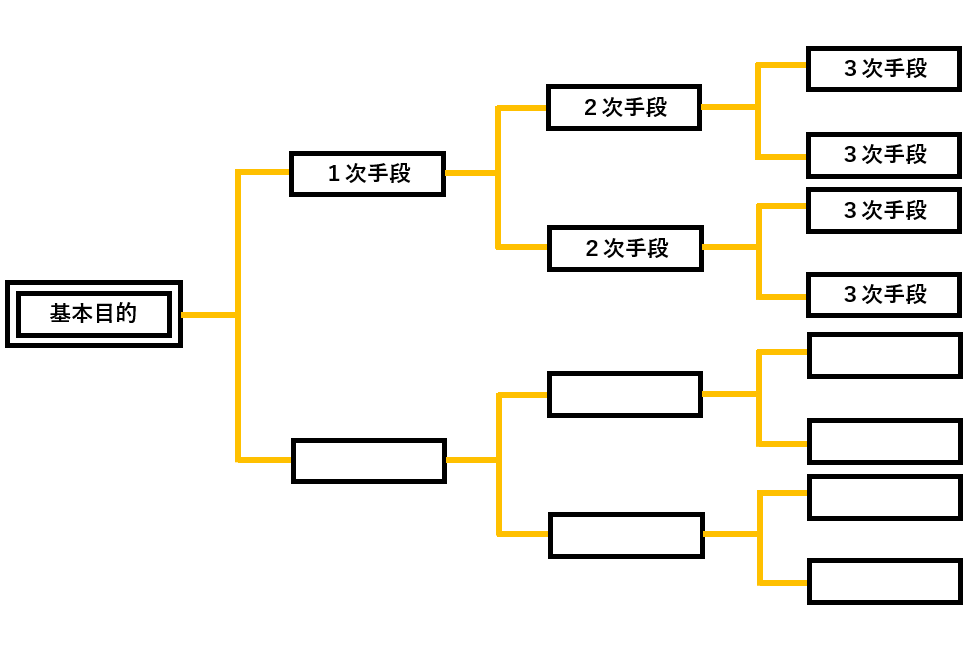
①目的と手段の関係を展開し、目的を達成するための最適手段を追求していく方法
（手法の名称：ア 概略図：イ）
②原因と結果が複雑に絡み合っている場合に、その関係を論理的につなぎ整理する方法
（手法の名称：ウ 概略図：エ）
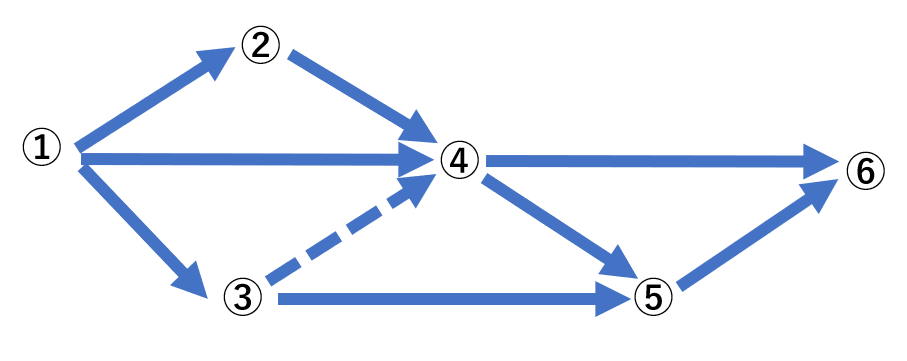
③計画を推進するのに必要な作業順序を矢線と結合線を用いた手法
（手法の名称：オ 概略図：カ）
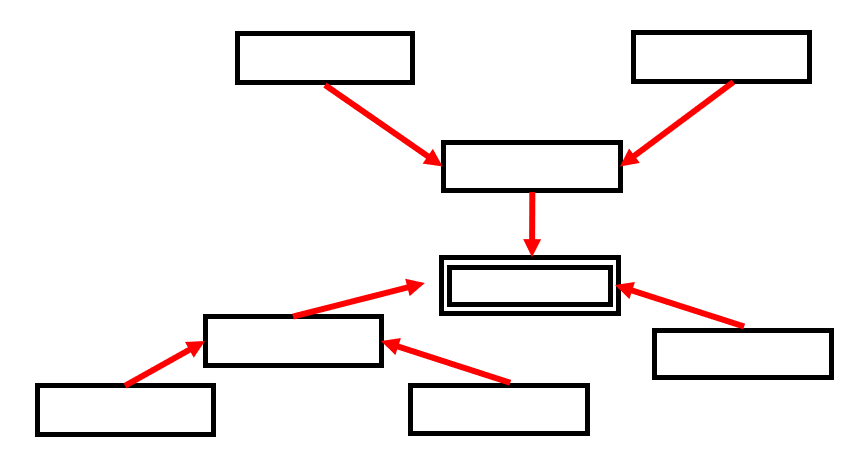
④将来の問題など、ハッキリしていない問題について、言語データとしてとらえ、それらの相互の親和性によって図で示し、問題の所在を明らかにしていく方法
（手法の名称：キ 概略図：ク）
【選択肢】
- 親和図法
- マトリックス図法
- アローダイヤグラム法
- 系統図法
- 連関図法
| 6 | 7 | 8 | 9 |
 |
 |
 |
 |
アローダイアグラムの例題解答
解答・解説（+クリック）
図法の意味や、それぞれの概略図などをイメージできるようにしておきましょう。
| 番号 | 手法の名称 | 概略図 |
| ① | ア：4.系統図法 | イ |
| ② | ウ：5.連関図法 | エ |
| ③ | オ：3.アローダイヤグラム法 | カ |
| ④ | キ：1.親和図法 | ク |
ちなみにアローダイアグラムは新QC七つ道具のひとつですので、他の図法も併せてチェックしておくとよいでしょう。
アローダイヤグラムの解き方をわかりやすく！例題②クリティカルパス
つづいてはネットワーク工程表（クリティカルパス）の問題です。
アローダイアグラムの例題
下図のネットワーク工程表に関する次の記述のうち、適当なものはどれか。
（平成28年 1級土木施工管理技士学科問題B No. 13)
- クリティカルパスは、⓪→①→②→④→⑤→⑨である。
- 作業Kの最早開始日は、工事開始後19日である。
- ①→⑥→⑦→⑧の作業余裕日数は4日である。
- 工事開始から工事完了までの必要日数（工期）は27日である。
アローダイアグラムの例題解答
解答・解説（+クリック）
〈解答・解説〉3
1.クリティカルパスは、⓪→①→②→④→⑤→⑨である。⇒×
クリティカルパスは１番日数がかかるもの。
したがって、それぞれのルートを計算してみると、
⓪→①→②→④→⑤→⑨＝27日（5+5+6+5+6）
⓪→①→②→④→⑤→⑧→⑨＝25日（5+5+6+5+4）
⓪→①→②→③→⑤→⑨＝29日（5+5+7+6+6）
⓪→①→②→③→⑤→⑧→⑨＝27日（5+5+7+6+4）
⓪→①→⑥→⑦→⑧→⑨＝23日（5+2+5+7+4）
したがって、クリティカルパスは⓪→①→②→③→⑤→⑨となる。
2.作業Kの最早開始日は、工事開始後19日である。⇒×
作業が複数あるときは、最早開始日は１番作業日数がかかるものであるから、
⑧（K）までのルートを計算してみると
⓪→①→②→④→⑤→⑧＝23日
⓪→①→②→③→⑤→⑧＝21日
⓪→①→⑥→⑦→⑧＝19日
したがって、最早開始日は23日である。
3.①→⑥→⑦→⑧の作業余裕日数は4日である。⇒〇
①から⑧にいくルートは３つ
⓪→①→②→④→⑤→⑧＝23日
⓪→①→②→③→⑤→⑧＝21日
⓪→①→⑥→⑦→⑧＝19日
したがって、23日－19日＝4日（作業余裕日数）
4.工事開始から工事完了までの必要日数（工期）は27日である。⇒×
必要日数はクリティカルパス（もっとも時間のかかるもの）と同じになるため、
⓪→①→②→③→⑤→⑨＝29日（5+5+7+6+6）となる。
（他のルート）
⓪→①→②→④→⑤→⑨＝27日（5+5+6+5+6）
⓪→①→②→④→⑤→⑧→⑨＝25日（5+5+6+5+4）
⓪→①→②→③→⑤→⑨＝29日（5+5+7+6+6）
⓪→①→②→③→⑤→⑧→⑨＝27日（5+5+7+6+4）
⓪→①→⑥→⑦→⑧→⑨＝23日（5+2+5+7+4）
【関連記事】
【簡単】ネットワーク工程表の解き方！クリティカルパスを見極めよ
アローダイヤグラムの解き方＆書き方をわかりやすくまとめ
以上です。
参考になればうれしいです。
ありがとうございました。