振り子とは、ばねや糸に重りをつるし、少し引っ張ってから離すと重りが振動する運動のことです。
周期の計算や振り子の法則についてサクッと解説していきます。
計算例題も載せておきましたので、ぜひチャレンジしてみてください。
目次
振り子の法則や周期計算とは?物理Ⅱわかりやすく例題付きで解説
振り子は以下のとおり2種類に分けることができます。
振り子の種類
- ばね振り子
- 単振り子
ばね振り子の法則と公式
ばねに重りをつるし、少し引っ張ってから放すと、重りが振動します。
この現象を【ばね振り子】といいます。
たとえば、ばね定数kのばねに質量mの重りをつるすと、ばねがx₀だけ伸びたとします。
このとき、フックの法則により
mg=kx₀
の関係が成り立ちます。
さらにこの重りに下向きの力fを加え、さらにばねをxだけ伸ばしたとすると、
f+mg=k(x₀+x)
となります。
一方で、力fを取り除いて、ばね振り子を振動させてみましょう。
力fを取り除いた直後の合力Fは、鉛直下向きを正とすると、
F=mg-k(x₀+x)=-kx
となるから、Fは重りのつり合いの位置から変位xに比例し、変位の向きと反対向きになっていることが分かります。
このFがばね振り子の復元力を表しています。
よって、上記の式から、ばね振り子の復元力の比例定数はばね定数に等しいので、ばね振り子の周期Tは、
T=2π√(m/k)
となります。
またばね振り子の振動数は周期の逆数です。
| ばね振り子の法則 | |
| ばね定数kのばねに質量mの重りをつるし、ばねがx₀だけ伸びたとき | mg=kx₀ |
| さらにこの重りに下向きの力fを加え、さらにばねをxだけ伸ばしたとき | f+mg=k(x₀+x) |
| 力fを取り除いた直後の合力F | F=mg-k(x₀+x)=-kx |
| ばね振り子の周期T | T=2π√(m/k) |
| ばね振り子の振動数 | f=1/T |
ばね振り子の計算例題
ココでひとつ、例題を解いてみましょう。
【例題】
ばねに重りをつるしたら、ばねは4.9cmのびてつり合った。この状態から、重りを上下に振動させたときの振動数はいくらか。
【解答】
重りの質量をm、ばね定数をkとすると、つり合ったときの式は、フックの法則より
mg=k×4.9×10⁻²
m/k=4.9×10⁻²/g=4.9×10⁻²/9.8=(1/2)×10⁻²
ばね振り子の周期は、
T=2π×√m/k=2×3.14×√((1/2)×10⁻²)
求める振動数fは周期の逆数であるから、
f=1/T=√2/(2×3.14×10⁻¹
=1.41/0.628=2.2
解答:2.2Hz
単振り子の法則と公式
重りを糸につるして左右に振らせるだけの簡単な振り子を【単振り子】といいます。
糸の固定点から重りの重心までの距離を振り子の長さとしています。
まずは、単振り子の復元力について考えてみましょう。
質量mの重りをつるした長さℓの単振り子について確認していきます。
糸が鉛直方向と角度θをなしているとき、糸の張力Sと重力mgの合力は、重りの軌道の接線方向を向いており、その大きさはmgsinθです。
この合力はつねに重りのつり合いの位置からの変位の向きと反対であるから、復元力としての働きはありますが、その大きさが変位に比例しないので、ばね振り子と同じようにはなりません。
また、単振り子の振幅が非常に小さい場合、重りの軌道も直線とみなすことができます。
それによって重りの軌道をx軸と考えると、重りの変位xは、θを[rad]で表して
x=ℓθ…①
となります。
また、θが非常に小さいため、sinθ≒θという近似も成り立ちます。
したがって重りに働く力の合力は、
F=-mgsinθ≒-mgθ…②
①②からθを消去すると、
F=-mgx/ℓ
となり、合力Fは変位xに比例する復元力であると言えます。
また、単振り子の周期は、単振り子の復元力比例定数はK=mg/ℓであるため、
T=2π√(m/K)=2π√(m/(mg/ℓ))
=2π√ℓ/g
となります。
| 単振り子の法則 | |
| 合力F
(sinθ≒θという近似も成り立つとき) |
F=-mgx/ℓ
ℓ:振り子の長さ、x:重りの変位、mg:重力 |
| 単振り子の周期T
(振幅が小さい時) |
T=2π√ℓ/g |
| 単振り子の振動数 | f=1/T |
単振り子の計算例題
【例題】
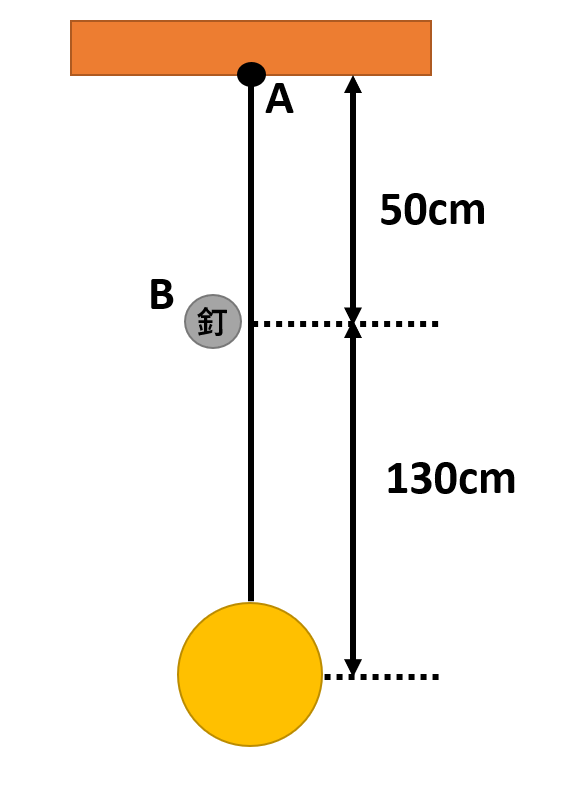
上記の図のように、長さ130cmの振り子をつくり、糸を点Aに固定します。点Aから鉛直下方50cmのところにくぎBを打ち、振り子が右から左に振れるとき、中心をすぎると糸がくぎBにひっかかるようにしておきます。
このとき、重りを右へわずかに引いて静かに手を離すと、重りは振動します。このときの振動の周期を求めなさい。
【解答】
この振り子は右半分では長さ130cmの単振り子となり、左半分では80cmの単振り子となるから、右と左の周期を別々に求めることがポイントです。
振り子が中心から右へ振れて再び中心へ帰るまでの時間t₁は、長さ130cmの単振り子の周期T₁の半分であるから、
t₁=T₁/2=(1/2)×2π√(ℓ₁/g)=3.14×√1.3/9.8=1.14(s)
この振り子が中心から左へ振れて再び中心へ帰るまでの時間t₂は、長さ80cmの単振り子の周期T₂の半分であるから、
t₂=T₂/2=(1/2)×2π√(ℓ₂/g)=3.14×√0.8/9.8=0.90(s)
よって求める周期はt₁とt₂の和に等しいため、
T=t₁+t₂=1.14+0.90=2.04(s)
解答:2.04秒
振り子の法則や周期計算とは?物理Ⅱわかりやすくまとめ
| ばね振り子の法則・計算公式 | |
| ばね定数kのばねに質量mの重りをつるし、ばねがx₀だけ伸びたとき | mg=kx₀ |
| さらにこの重りに下向きの力fを加え、さらにばねをxだけ伸ばしたとき | f+mg=k(x₀+x) |
| 力fを取り除いた直後の合力F | F=mg-k(x₀+x)=-kx |
| ばね振り子の周期T | T=2π√(m/k) |
| ばね振り子の振動数 | f=1/T |
| 単振り子の法則・計算公式 | |
| 合力F
(sinθ≒θという近似も成り立つとき) |
F=-mgx/ℓ
ℓ:振り子の長さ、x:重りの変位、mg:重力 |
| 単振り子の周期T
(振幅が小さい時) |
T=2π√ℓ/g |
以上です。
ありがとうございました。
.png)