正規分布とは？わかりやすく標準偏差との関係や見方をていねい解説

正規分布って何？わかりやすく教えて…

こんなお悩みに！

初心者向けに、正規分布や標準偏差をわかりやすく解説します。

それではさっそく参りましょう、ラインナップはもくじからどうぞ 🙂

正規分布とは？わかりやすくかんたん解説

正規分布とは、以下のように左右対称のつり鐘型の分布を示したグラフのことです。

特徴はこんな感じ 🙂

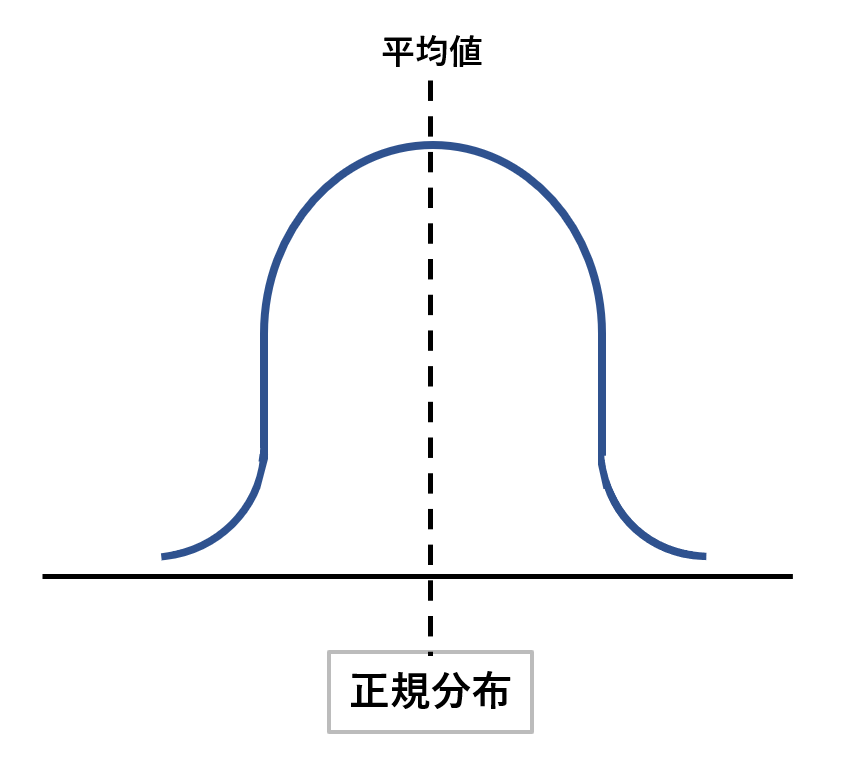
異常原因がなく、偶然原因だけによるバラツキ状態で、このときの管理状態は安定しており、もっとも理想的な分布を表しています。

ちなみに平均が0で分散が1の正規分布は「標準正規分布」と呼ばれます。

たとえば正規分布が使用されるのは、技術系（土木や機械）の製品生産などにおいてです。

品質に一定のバラツキが生じるのは避けられません。

ただ、そのバラツキには原因が2種類あり、許容されるバラツキ原因と取り除くべきバラツキ原因があります。

品質のバラツキにも許容される原因（偶然原因）とそうでない原因（異常原因）があるんだね

正規分布と標準偏差の関係をわかりやすく解説

正規分布と標準偏差の関係から、データ分布のパーセンテージが求められます。

標準偏差とは基本統計量のひとつで、【データが平均値の周辺でどれくらいばらついているか】を表します。

標準偏差は平均値では表せないデータのバラツキを知るための便利なツールです。

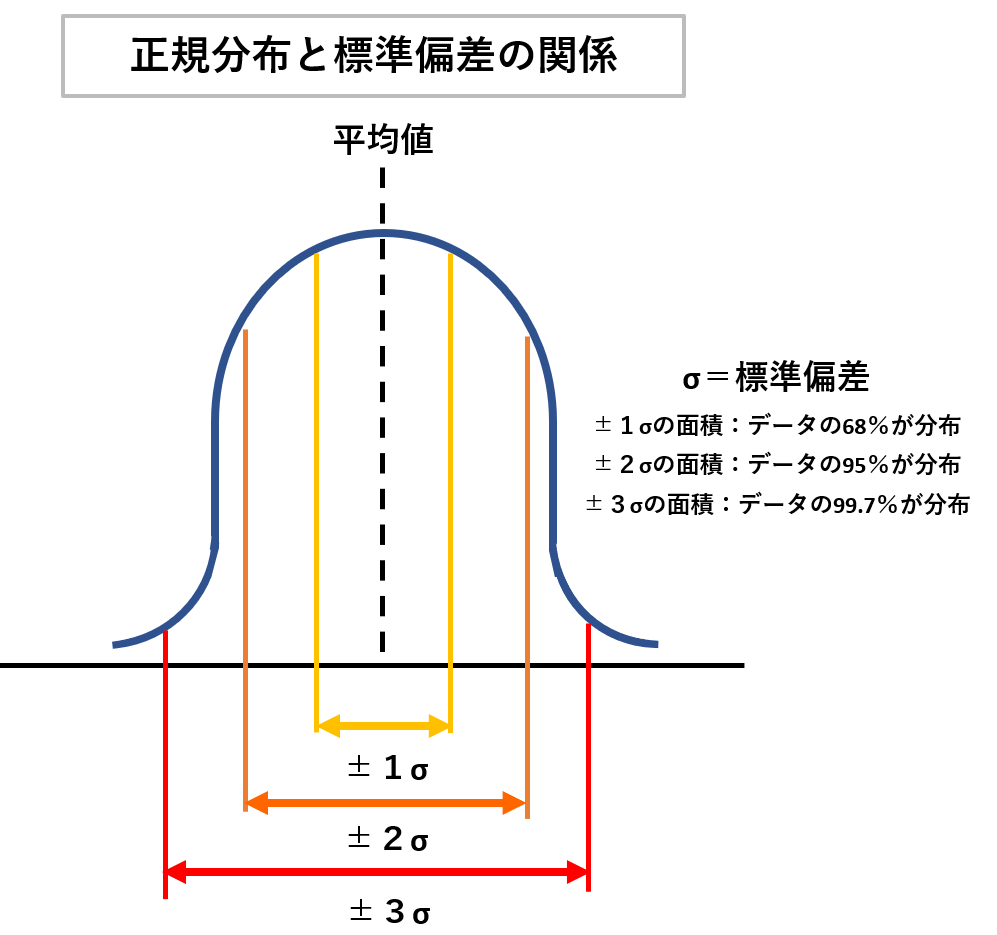
それぞれのグラフ面積（標準偏差）と関係する、データ数のパーセンテージは以下のとおり。

つまり標準偏差がわかれば、そのグラフ範囲にどれくらいの観測データが含まれているかが把握できるのです。

正規分布には欠かせない！標準偏差の計算方法

正規分布を語るうえで、標準偏差の計算方法は知っておくべきものです。

標準偏差の計算方法は次の3ステップ 🙂

しっかりチェックしておきましょう。

1.平方和S（残差平方和）を求める

まずは残差平方和Sを求めます。

残差平方和とは、個々のデータの平均値と各データの差を2乗したものの和のことです。

残差平方和はデータと推定モデルとの差異（ズレ）を評価している尺度のこと

たとえばデータ（サンプル）数が3、4、6、7、10とすると、

平均値は6なので、

式　S＝(10-6)²+（7-6)²+(6-6)²+(4-6)²+(3-6)²=30

残差平方和は30となります。・・・①

2.不偏分散Vを求める

次に不偏分散Vを求めます。

不偏分散とは、知りたい対象の一部（標本）から、知りたい対象のすべて（母集団）の分散を推定するために用いられるもの

不偏分散Vは、残差平方和Sを（データ数-1）で割ったものです。

よって①で求めたSを使って式を表すと、

式　V＝30÷（5-1）＝7.5・・・②

3.標準偏差σを求める

さいごにやっと標準偏差（笑）

標準偏差は、不偏分散の正の平方根のこと。

データのバラツキを調べるためにもっともよく使われる公式です。

②で求めた不偏分散を代入すると、

式　σ＝√7.5＝2.74・・・③

標準偏差は2.74であることが求められました。

ちなみに標準偏差が大きくなると、正規分布は左右の広がっていき、標準偏差が小さくなると、正規分布は上に鋭く尖った形になります。

正規分布をわかりやすく＆標準偏差の計算方法まとめ

正規分布とは、左右対称のつり鐘型の分布を示したグラフのことで、形は平均と標準偏差によって決まる

異常原因がなく、偶然原因だけによるバラツキ状態で、このときの管理状態は安定していてもっとも理想的な分布

データのバラツキには許容される偶然原因と取り除くべき異常原因の2種類がある

正規分布と標準偏差の関係から、データ分布のパーセンテージが求められる

標準偏差がわかれば、どの範囲にどれくらいの観測データが含まれているかが分かる

平均が0で、分散が1のものを「標準正規分布」とよぶ

標準偏差の計算方法（3ステップ）

以上です。

いっぽう、関連として以下の記事もおすすめです。

ヒストグラムの作り方かんたん解説★技術系品質管理の基礎知識

管理図の種類★覚え方＆見方ていねい解説【例題あり】

工程能力図とは？品質管理（土木）でよく使う変動データの表示法

興味のある方はぜひどうぞ 🙂

ありがとうございました。