フックの法則とは、【ばねの伸びは引っ張る力に比例する】という法則です。
この記事ではフックの法則や公式をわかりやすく解説していきます。
さらに数式やひずみとの関係公式も簡単に解説しますのでぜひどうぞ!
目次
フックの法則公式や伸び・ひずみの公式について!わかりやすく簡単に解説
フックの法則公式についてみていきましょう。
フックの法則の定義
冒頭でも話したように、フックの法則とは、【ばねの伸びは引っ張る力に比例する】という法則です。
たとえば、ばねにF【N(ニュートン)】の力を加えたとき、x【m】伸びた(または縮んだ)とすると、
ポイント
公式:F=kx
(※k[N/m]:ばね定数)
が成り立ちます。
この公式はしっかり覚えましょう。(文字の部分に数値が入ると数式となる)
ばね定数kが大きいほど、ばねを伸ばすために大きな力が必要になります。
フックの法則や公式・数式をわかりやすく解説!

つづいてはフックの法則について、公式を確認していきましょう。
フックの法則は、ばねの伸び縮みの関係のほか、物体に加えた応力とそれに対応して生ずるひずみとの間での数式(公式)が成り立ちます。
ポイント
公式:F=kx
(F=力、k=ばね定数、x=ばねの伸びた(縮んだ)長さ)
公式:σ=Eε
(σ=垂直応力、E=ヤング率または縦弾性係数、ε=垂直ひずみ)
応力とひずみの関係が成立する限界の応力を【比例限度】とよびます。
一方で、長さLで一様な断面積Aをもつ棒が荷重Pを受けδだけ縮む場合に適用すると、フックの法則は以下のとおりとなります。
ポイント
公式:δ=PL/AE
(δ=棒が伸びた長さ、P=荷重、A=棒の断面積、L=棒の長さ、E=ヤング率または縦弾性係数)
つまり棒の変形はPとLに比例し、AとEに反比例することがわかりますね 🙂
フックの法則公式と伸び・ひずみの関係をわかりやすく簡単に!
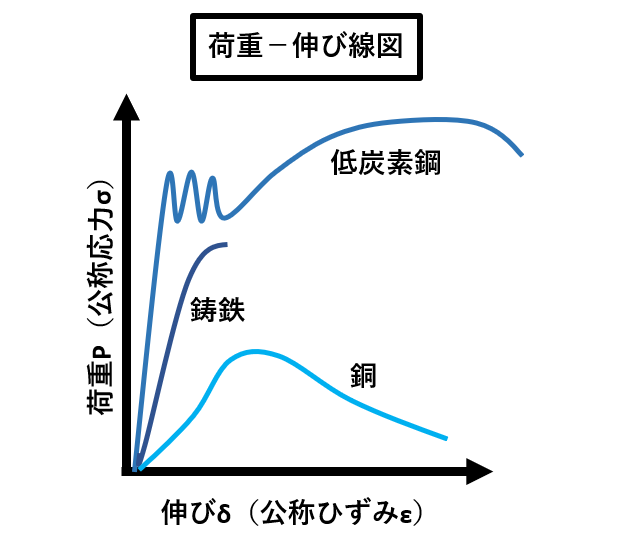
一方で、フックの法則はせん断応力τとせん断ひずみγについても公式が成り立ちます。
せん断応力の計算や応力ひずみ線図も併せてチェックしておいてください。
ポイント
公式:τ=Gγ
(τ=せん断応力、G=横弾性係数(せん断弾性係数)、γ=せん断ひずみ)
ちなみにGの横弾性係数やEのヤング率は材料固有の値となり、例えば工業材料の機械的性質は以下のとおりです。
ポアソン比とヤング係数(率)には深い関係があります。
| 材料 | 縦弾性係数
E(GPa) |
横弾性係数
G(GPa) |
ポアソン比
ν |
降伏点(体力)
σ₁(MPa) |
引張強さ
σ₂(MPa) |
| 軟鋼
(0.1~0.3%C) |
206 | 80 | 0.3 | 245 | 392 |
| 硬鋼
(0.4~0.6%C) |
206 | 80 | 0.3 | 372 | 490 |
| Ni-Cr鋼(熱処理) | 206 | 80 | 0.3 | 686 | 882 |
| 鋳鋼 | 206 | 80 | 0.3 | 343 | 588 |
| 鋳鉄 | 98 | 34 | 0.3 | 157 | 196 |
| 銅 | 126 | 46 | 0.33 | 軟質:88 | 軟質:225 |
| 硬質:294 | 硬質:314 | ||||
| アルミニウム | 69 | 27 | 0.33 | 軟質:29 | 軟質:69 |
| 硬質:127 | 硬質:137 | ||||
| ジュラルミン | 69 | 27 | 0.33 | 245 | 294 |
| 鉛 | 17 | 7.6 | 0.45 | - | 20 |
| ガラス | 69 | - | 0.22 | - | 39 |
| 合成樹脂 | 4 | - | 0.3 | - | 69 |
一方、たとえば水中の部材が受ける水圧など、部材が一様な圧力P(N/㎡)を受けて体積ひずみεvが生じた場合のフックの法則は以下のとおりです。
ポイント
公式:-P=Kεv
(P=圧力、K=体積弾性率、εv=体積ひずみ)
この体積弾性率Kも、EやGと同じく使用する材料によって定まった値をもち、それぞれの弾性定数の間には次の公式(数式)が成り立ちますので覚えておくとよいでしょう。
ポイント
公式:G=E/2×(1+ν)
公式:K=E/3×(1-2ν)
※ν=ポアソン比

フックの法則公式や伸び・ひずみの公式まとめ

フックの法則に関連する公式を一覧表にまとめましたので、ぜひチェックしてみてください。
| フックの法則(公式・数式)ひずみとの関係 | 概要 |
| F=kx | ばねにF【N(ニュートン)】の力を加えたとき、x【m】伸びた(または縮んだ)とする
F=力、k=ばね定数、x=ばねの伸びた(縮んだ)長さ |
| σ=Eε | σ=垂直応力、E=ヤング率または縦弾性係数、ε=垂直ひずみ |
| δ=PL/AE | δ=棒が伸びた長さ、P=荷重、A=棒の断面積、L=棒の長さ、E=ヤング率または縦弾性係数 |
| τ=Gγ | τ=せん断応力、G=横弾性係数(せん断弾性係数)、γ=せん断ひずみ |
| -P=Kεv | P=圧力、K=体積弾性率、εv=体積ひずみ |
| ※参考
G=E/2×(1+ν) K=E/3×(1-2ν) |
G=横弾性係数(せん断弾性係数)
E=ヤング率または縦弾性係数 K=体積弾性率 ν=ポアソン比 |
以上です。
ありがとうございました。
