
せん断力、またはせん断応力とは、せん断荷重(面と平行方向の力)をかけたときに、その面にすべらせるように作用する応力(物体内部にかかる力)のことです。
たとえば、はさみで紙を切ろうとするときに、はさみの両刃が紙に作用する力のことを【せん断応力】と呼んでいます。(以下イメージ図参照)

切断しようとする紙の微小な部分を上下から両刃が押し込むことで発生する力とも言えますね。
というわけで、今回のテーマは【せん断力、せん断応力の求め方】
例題で計算や単位についても解説していますのでぜひチェックしてみてください。
目次
せん断力・せん断応力の求め方!計算公式と単位について
せん断応力τ(タウ)を求める計算式は
【せん断応力τ(MPa)=せん断荷重W(N)÷断面積A(m㎡)】
せん断荷重を断面積で割り算します。
単位はMPa(メガパスカル)で表すことが多いです。

せん断力・せん断応力の求め方!計算例題で単位もしっかりチェック
ここでひとつ、計算例題を解いてみましょう。
せん断力・せん断応力の計算例題
【計算例題】
荷重5,000Nがかかる一辺10mmの正方形にかかるせん断応力τを求めなさい。
せん断力・せん断応力の計算解答
最大せん断応力の求め方!計算公式と断面形状
ちなみに、前章までで求めているのは正確には「平均せん断応力」といいます。
実際には部材の断面に均一に50 MPaの応力が発生するわけではなく、中央部が大きく、端っこに行くにつれ応力は小さくなります。
断面中に発生する一番大きい応力を「最大せん断応力」と呼び、平均せん断応力よりも大きな値となります。
より正確に計算する場合は「最大せん断応力」を求める必要があることを覚えておきましょう。
以下に代表的な断面の(最大)せん断応力の公式をまとめておきましたので参考にしてください。
| 断面形状 | (最大)せん断応力 | 記号の定義 |
| 長方形
|
τmax=3W/2bh=τmean×3/2 | τmax 最大せん断応力 [MPa]
τmean 平均せん断応力 [MPa] W 荷重(せん断力) [N] b はりの幅 [mm] h はりの高さ [mm] |
| 円形
|
τmax=τmean×4/3 | τmax 最大せん断応力 [MPa]
τmean 平均せん断応力 [MPa] |
H型断面(ウェブ部のせん断応力).png) |
τw(y₁) =FSz(y₁)/Izt=F/tIz{t/2(h₂²/4-y₁²)+b/8(h₁²-h₂²)} | τw(y₁) y₁の位置のウェブ部のせん断応力 [MPa]
F せん断力 [N] h₁ 全体の高さ [mm] b 全体の幅 [mm] t ウェブの幅 [mm] h₂フランジ間の高さ [mm] y₁ 中立軸からの位置 [mm] Sz(y₁) y₁の位置の断面一次モーメント [mm3] Iz 断面二次モーメント [mm4] |
| H型断面(フランジ部のせん断応力)
|
τF(y₁)=FSz(y₁)/Izb=F/2Iz(h₁²/4-y₁²) | τF(y₁) y₁の位置のフランジ部のせん断応力 [MPa]
F せん断力 [N] h₁ 全体の高さ [mm] b 全体の幅 [mm] t ウェブの幅 [mm] Sz(y₁) y₁の位置の断面一次モーメント [mm3] Iz 断面二次モーメント [mm4] |
せん断力・せん断応力の求め方!応力図でわかりやすく解説
こちらも参考ですが、はり静定物においての応力図についてまとめました。
せん断応力図にくわえ、曲げモーメント図も合わせて覚えておくと良いでしょう。
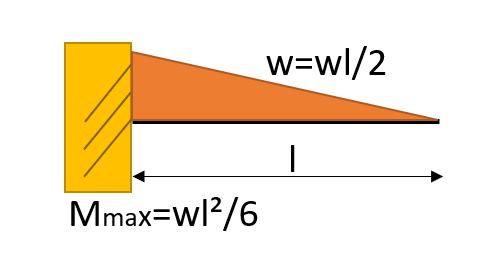
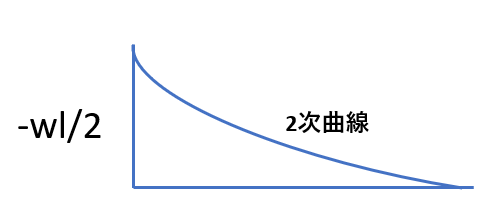
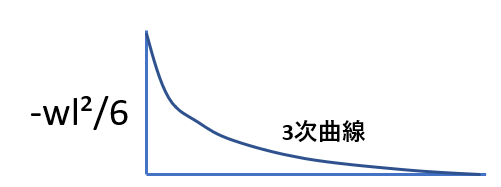
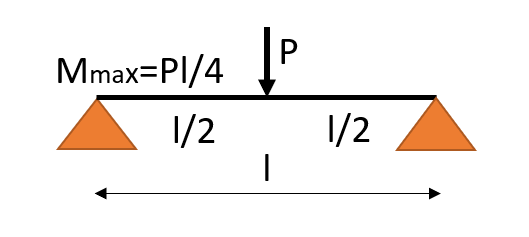
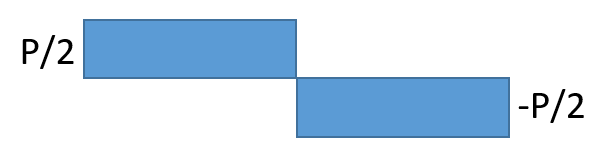
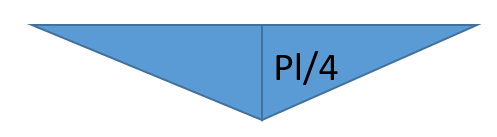
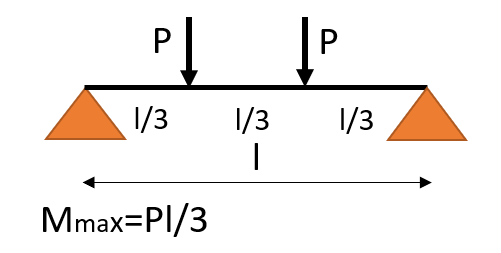
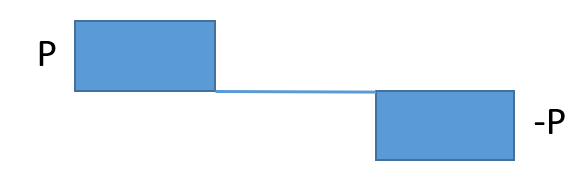
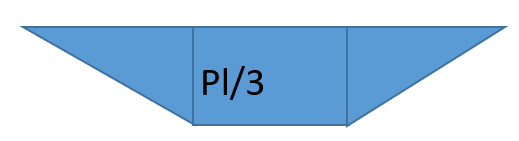
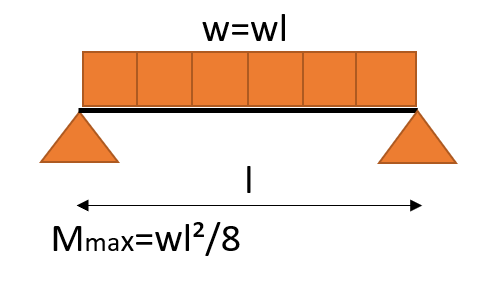
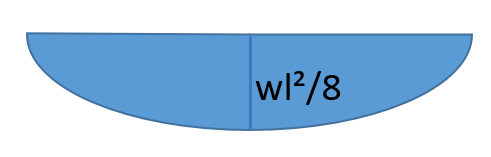
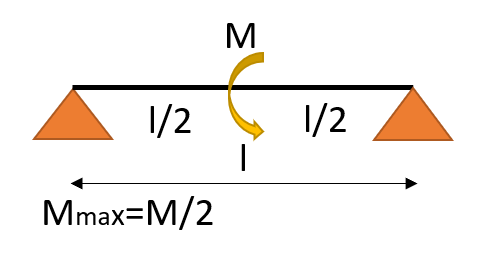
| 荷重条件・公式 | せん断応力図 | 曲げモーメント図 |
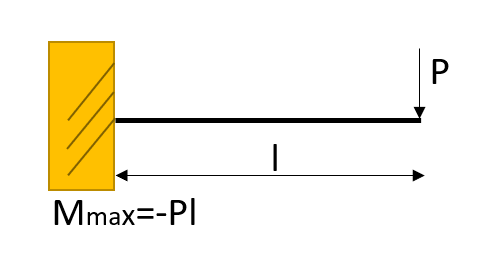 |
 |
 |
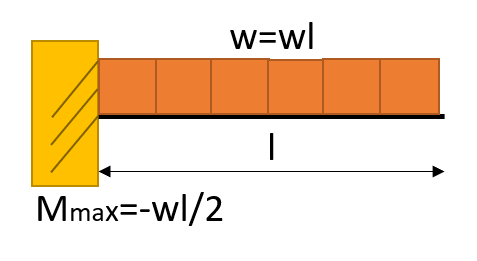 |
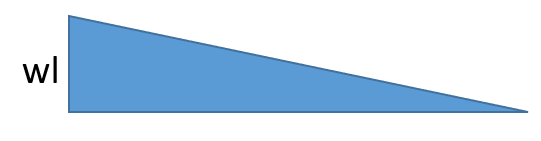 |
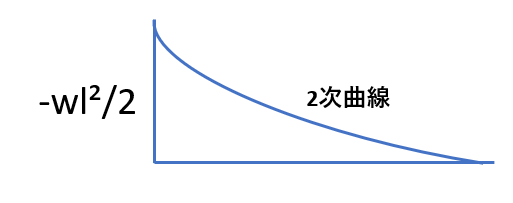 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |

せん断力・せん断応力の求め方!計算例題で単位と公式まとめ
【せん断応力τ(MPa)=せん断荷重W(N)÷断面積A(m㎡)】
- せん断荷重を断面積で割り算
- 単位はMPa(メガパスカル)で表すことが多い
最大せん断応力は図形の形によって公式が異なる
せん断応力図も併せてチェックしておくとよい
以上です。
ありがとうございました。

.png)
.png)