今回のテーマは【線膨張係数αと熱応力σ】
例題を使って解説していきますのでぜひチェックしてみてください。
目次
線膨張係数と熱応力★定義と公式
一般的に固体(物体)は温度が上がれば膨張し、温度が下がれば収縮する性質があります。
この温度変化による固体の自由な膨張または収縮が、何かしらの拘束によって妨げられると、固体内に妨げられた変形量に対する応力が発生します。
この応力を【熱応力(thermal stress)】といいます。
例えば、橋(鉄骨)などをつくるときには、夏や冬の気温の変化によって橋が膨張したり縮んだりするため、余裕(スキマ)を考慮した「伸縮装置」というものが設置されます。
.jpg)
【橋の伸縮装置】
一方で、熱応力で生じる温度1℃の変化に伴う単位長さ当たりの変形量を【線膨張係数(coefficient of linear expansion)】といいます。
20℃における一般的な工業材料の線膨張係数αの値は以下の一覧表を参考にしてください。
| 材料 | 線膨張係数(20℃)
α(×10⁻⁶)1/℃ |
| 軟鋼 | 11.2 |
| 硬鋼 | 10.7 |
| 鋳鉄 | 8.7~11.1 |
| 金 | 14.2 |
| 銀 | 18.9 |
| 銅 | 16.6 |
| 亜鉛 | 33.0 |
| アルミニウム | 23.0 |
| ジュラルミン | 22.6 |
| ニッケル | 12.8 |
| マグネシウム | 25.6 |
| 黄銅 | 18.0~23.0 |
| はんだ(白ろう) | 25.0 |
| ポリエステル | 55~100 |
| ポリ塩化ビニル | 70~80 |
| メタクリル | 70~90 |
| ガラス | 9~10 |
| コンクリート | 7~13 |
| 弾性ゴム | 77 |
| 木材(縦) | 3~5 |
| 木材(横) | 35~60 |
| れんが | 3~9 |
たとえば、以下の図のように、長さℓの棒材が両端を間隔一定の剛体壁に固定された場合を考えてみましょう。
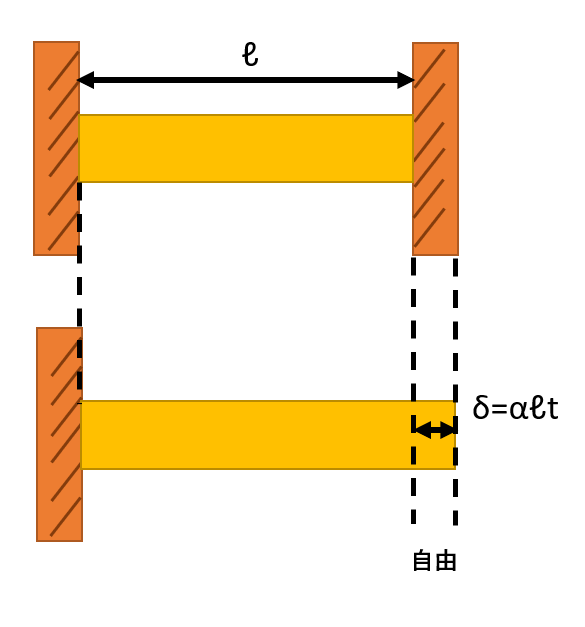
この棒材を加熱して温度をt℃上昇させたとします。
もし、このとき棒材の右端が自由であるなら、図のように自由に膨張してδ伸びることになります。
この伸びδは、
δ=線膨張係数×棒材の長さ×上昇(下降)温度
=αℓt
として計算することができます。
一方で、以下の図のように棒材が両端を間隔一定の剛体壁に固定されているときは伸びることができません。
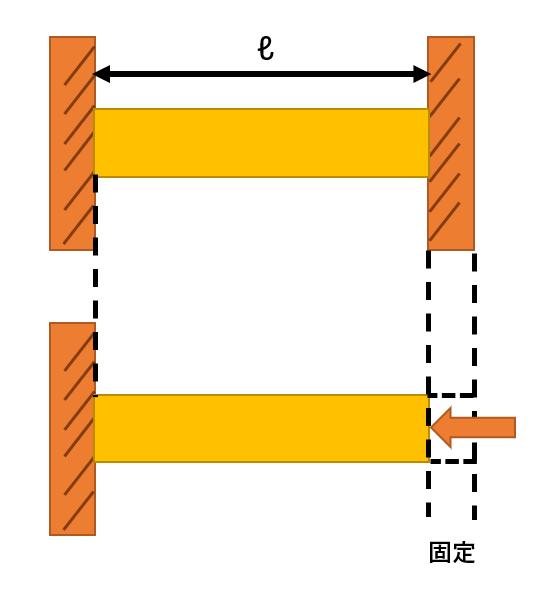
その場合、長さℓ+αℓtの棒材が圧縮荷重を受けてαℓtだけ縮められ、原長ℓの長さにされたものと考えることができます。
よってそのときの圧縮ひずみεは、
ε=-αℓt/ℓ+αℓt=-αt/1+αt
分母のαtは1に比較して微小であるから省略でき、
ε=-αt
これにより棒材に生じる圧縮応力(熱応力)σは以下の式となります。
σ=Eε=-Eαt
このように棒材に温度変化があったとき、外力を加えないのに上記の式で与えられるような熱応力が発生するわけです。
【例題】線膨張係数と熱応力
ここでひとつ、例題を解いてみましょう。
【例題】
温度30℃のとき、長さ30mのレールが連続してスキマなく敷かれています。
温度が60℃になったときのレールに生じる熱応力を求めなさい。
また、温度が-20℃に下がったときのレールの縮みδはいくらか。
レールのヤング率E=200GPa、線膨張係数α=11×10⁻⁶/℃とします。

【解答】
①温度上昇による熱応力σは、公式より
σ=-Eαt=200×10⁹×11×10⁻⁶×(60-30)=-66MPa
②-20℃になったときのレールの縮みδは、公式より
δ=αℓt=-11×10⁻⁶×(-20-30)×30=16.5×10⁻³m=16.5mm
温度上昇によってレールのスキマがなくなり、自由な膨張が妨げられたレールには大きな圧縮(熱)応力が生じます。
解答 熱応力σ=-66MPa、縮みδ=16.5mm
以上です。
【関連記事】
- 断面係数の計算★公式や計算例かんたんチェック(一覧表付き)
- 座屈(ざくつ)とは?オイラー公式&座屈を種類別にかんたん解説
- ポアソン比とヤング係数の関係★工業材料別にかんたんまるわかり
- せん断応力の計算例題と単位|よくわかる力の基礎知識
- 応力ひずみ線図★用語や定義&材質別まとめ
- 曲げモーメントについて★パッと見分かる曲げモーメント図付き
- 応力とは?単位や種類・関連公式かんたんまるわかり
ありがとうございました。
