断面二次モーメントT型や断面係数の公式とは？図形別の求め方もチェック！

断面二次モーメントや断面係数の公式が知りたい

断面係数とは部材や構造物の断面性能を表すもので、構造力学の基礎となる用語です。

モーメントに対する強さ・抵抗力とも言い換えられますね。

そんなわけで今回は、いろいろな形の構造物別に、断面係数の計算方法や断面二次モーメントの公式について解説していきます。

それではさっそく参りましょう、ラインナップは目次からどうぞ！

断面二次モーメントT型や断面係数の公式とは？図形別の求め方もチェック！

今回ご紹介する構造物は以下のとおり。

断面係数Zの公式は【Z＝bh²/6（長方形断面のとき）】や【Z=I/y】です。

bは断面の幅、hは断面高さ、Iは断面二次モーメント、ｙは断面の中立軸から上端（下端）までの距離！

なお、Z＝I/yは断面係数の一般式で、断面の形状ごとに断面二次モーメントＩは異なります。

よって断面係数のほか、関連する断面二次モーメントと断面積の計算も合わせて載せておきます。

一方、曲げモーメントについてはまた別記事でまとめていますのでぜひどうぞ(^^♪

断面二次モーメント＆断面係数➀四角形・長方形・正方形

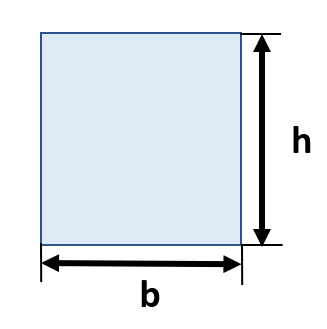
断面積A=b×h

断面二次モーメントI=(b×h³/12)

断面係数Z=(b×h²/6)

断面二次モーメント＆断面係数②三角形

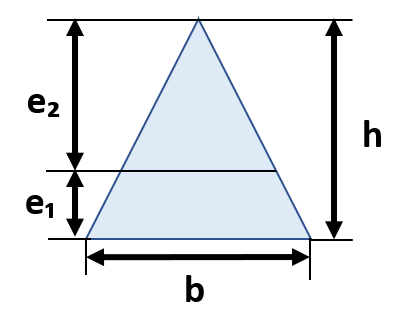
断面積A=b×h/2

断面二次モーメントI=(1/36)×bh³

断面係数Z₁=(bh²/12)、Z₂＝1/24bh²（e₁＝1/3h、e₂＝2/3h）

断面二次モーメント＆断面係数③円

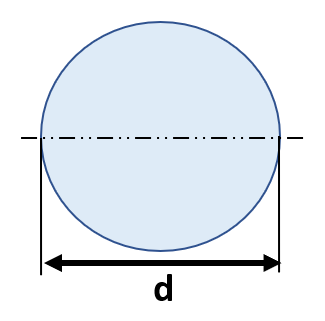
断面積A=πd²/4

断面二次モーメントI=πd⁴/64

断面係数Z=πd³/32

断面二次モーメント＆断面係数④二重円・中空円

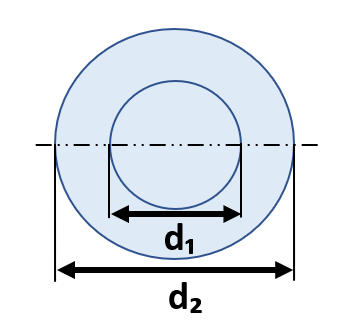
断面積A=1/4×π×(d₂²―d₁²)

断面二次モーメントI=π×(d₂⁴ーd₁⁴)

断面係数Z=(π/32)×(d₂⁴ーd₁⁴)/d₂

断面二次モーメント＆断面係数⑤楕円

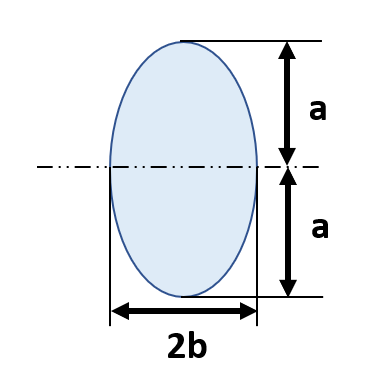
断面積A=abπ

断面二次モーメントI=π/4a³b

断面係数Z=π/4a²b

断面二次モーメント＆断面係数⑥コ・C型

断面積A=2×a×s+b₁×t

断面二次モーメントI=(a×b³－(a－t)×b₁³)/12

断面係数Z=(a×b³－(a－t)×b₁³)/6×h

断面二次モーメント＆断面係数⑦U型

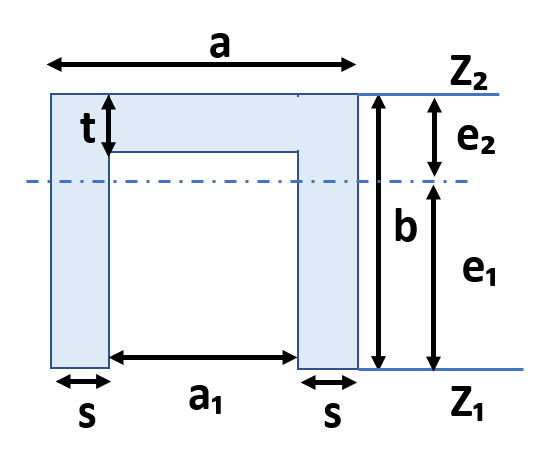
断面積A=2×b×s+a₁×t

e₁=b-e₂

e₂=(2×b²×s+a₁×t²)/(4×b×s+2×a₁×t)

断面二次モーメントI=(2×b³×s+a₁×t³)/3-A×e₂²

断面係数Z₁=I/e₁

断面係数Z₂=I/e₂

断面二次モーメント＆断面係数⑧T型

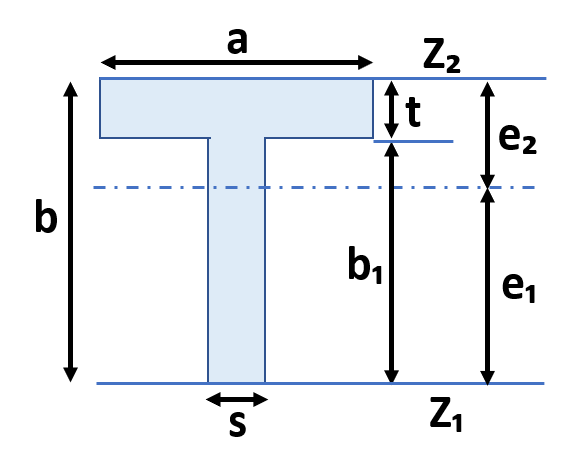
断面積A=a×t+b₁×s

e₁=b-e₂

e₂=(b²×s+(a-s)×t²)/(2×(a×t+b₁×s))

断面二次モーメントI=(b³×s+(a-s)×t³) /3－(A×e₂²)

断面係数Z₁=I/e₁

断面係数Z₂=I/e₂

断面二次モーメント＆断面係数⑨H型

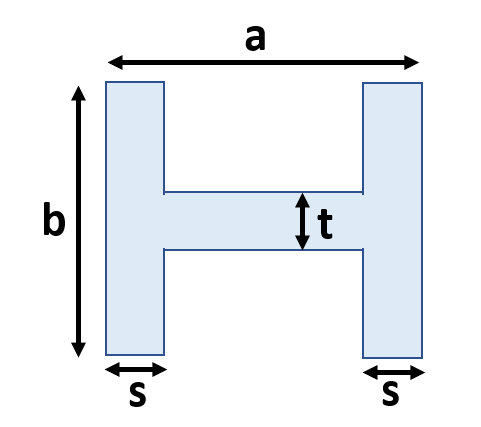
A=2×b×s+(a-2s)×t

I=(2×b³×s+(a-2s)×t³)/12

Z=(2×b³×s+(a-2s)×t³)/(6×h)

断面二次モーメント＆断面係数⑩I型

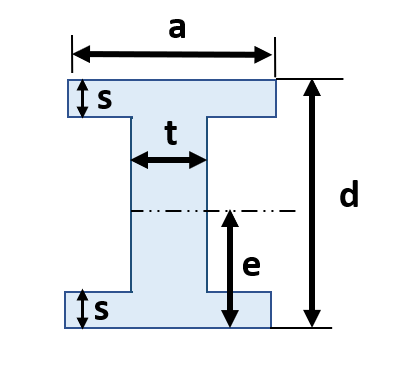
断面積A=ad-｛（a-t)×（d-2s）｝

断面二次モーメントI={ad³－h³(a－t)}/12

断面係数Z={ad³－h³(a－t)}/6d

断面係数＆断面二次モーメントの公式一覧表まとめ！T型や三角形など

断面の形と断面積	断面二次モーメント 【I】	断面係数Ｚ 【断面幅×高さ²/6】 【断面二次モーメント/断面の中立軸から上端（下端）までの距離】
A=b×h	b×h3/12³	b×h2/6
A=b×h/2	bh³/36	e₁＝1/3h、e₂＝2/3h、Z₁=1/12bh²、Z₂＝bh²/24
A=πd2/4	π/64d⁴	π/32d³
A=1/4×π×(d₂2―d₁2)	π（d₂⁴ーd₁⁴）	(π/32)×(d₂⁴ーd₁⁴)/d₂
A=abπ	π/4a³b	π/4a²b
A=2×a×s+b₁×t	I=(a×b3－(a－t)×b₁3)/12	Z=(a×b3－(a－t)×b₁3)/6×h
A=2×b×s+a₁×t	e₁=b―e₂ e₂=(2×b2×s+a₁×t2)/(4×b×s+2×a₁×t) 断面二次モーメントI=(2×b3×s+a₁×t3)/3－A×e₂2	断面係数Z₁=I/e₁ 断面係数Z₂=I/e₂
A=a×t+b₁×s	e₁=b-e₂ e₂=(b2×s+(a-s)×t2)/(2×(a×t+b₁×s)) I=(b3×s+(a-s)×t3) /3－(A×e₂2)	Z₁=I/e₁ Z₂=I/e₂
A=2×b×s+(a-2s)×t	I=(2×b3×s+(a-2s)×t3)/12	Z=(2×b3×s+(a-2s)×t3)/(6×h)
A=ad-｛（a-t)×（d-2s）｝	{ad³－(a-t)×（d-2s)³}/12	{ad³－(a-t)×（d-2s)³}/6d

以上です。

ありがとうございました。