たとえば、長い物差しに圧縮荷重をかけていくと突然曲がり、肉厚の薄いパイプをねじると表面に凹凸の変形を生じます。
このとき、材料は破損したわけではなく、それらは「構造として圧縮荷重を支える能力をなくした」というのが正しい見解です。
そしてこの「構造として圧縮荷重を支える能力をなくした」現象を【座屈(ざくつ)】と呼びます。
とくに細長い部材や薄肉の部材を設計するときには座屈が起こらないように気を付けなければいけません。
そんなわけでこの記事では、座屈の種類~公式までサクッと解説しています。
それではさっそく参りましょう、ラインナップは目次からどうぞ!
目次
座屈の種類!局部座屈や計算例・オイラー座屈公式もまとめてチェック
座屈とは、細長い部材や薄い部材に上から荷重を加えたときに、ある一定の荷重を超えると急に部材にたわみが生じる現象のことです。
座屈と一言で言っても、実は種類がいくつかあります。
座屈の種類
- 弾性座屈(オイラー座屈)
- 非弾性座屈
- 横座屈
- 局部座屈
また座屈を引き起こす荷重の大きさを「座屈荷重」といい、座屈したときに部材にかかる応力を「座屈応力」といいます。
| 座屈の種類 | 定義 |
| 弾性座屈 | 弾性座屈とは、加える力が大きくなっても部材の特性が弾性範囲内にあって初期状態を維持すること |
| 非弾性座屈 | 非弾性座屈とは、部材の特性が弾性範囲を超えて初期状態から変化すること |
| 横座屈 | 横座屈とは、部材が曲がってねじれることにより、横方向にはらみ出すように変形すること |
| 局部座屈 | 局部座屈とは、部材の一部分が局部的に膨らんだりへこんだりすることで、薄い部材で起こる場合が多い座屈 |
高速道路やビル、堤防などの構造物において座屈が想定される場合は、
- 座屈が生じやすい箇所に補強材を追加する
- 剛性の高い部材を採用する
- 断面二次モーメントを大きくする
などの対応が必要になります。
いっぽう座屈は、オイラーの公式を使って計算することができ、公式は以下のとおりです。
座屈荷重Pcr=Kπ²EI/ℓ²
座屈応力σ=Kπ²E/λ²
- Pcr:座屈荷重(座屈耐力)
- E:ヤング係数
- I:断面二次モーメント
- ℓ=長柱の長さ
- K=固定係数
- λ :柱の細長比(λ=l / i)
- i :断面2次半径(i = √I/A)
- A :柱の断面積
単位はN、またはkNです。
固定係数は柱の両端の端末条件などで決まります。
| 固定係数 | 端末条件 |
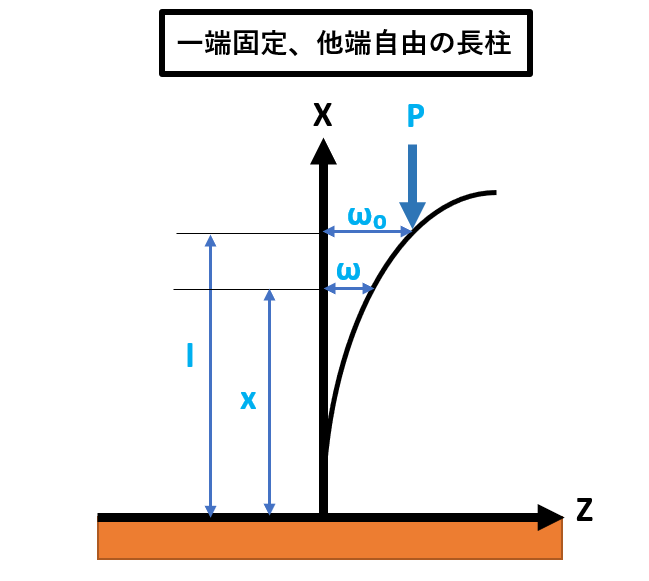
| K=1/4 | 一端固定かつ他端自由 |
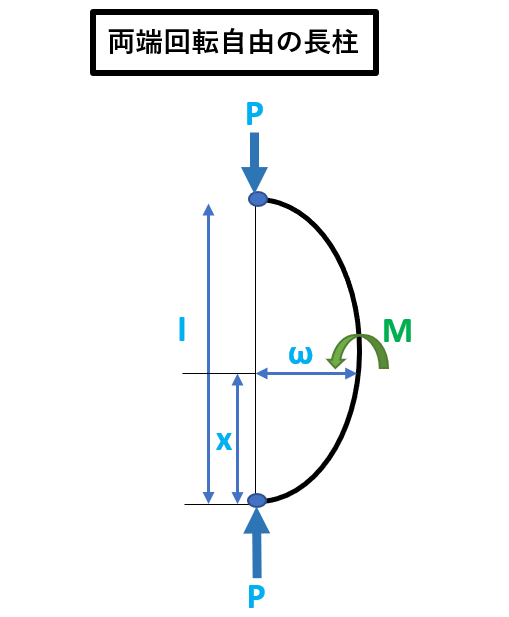
| K=1 | 両端回転 |
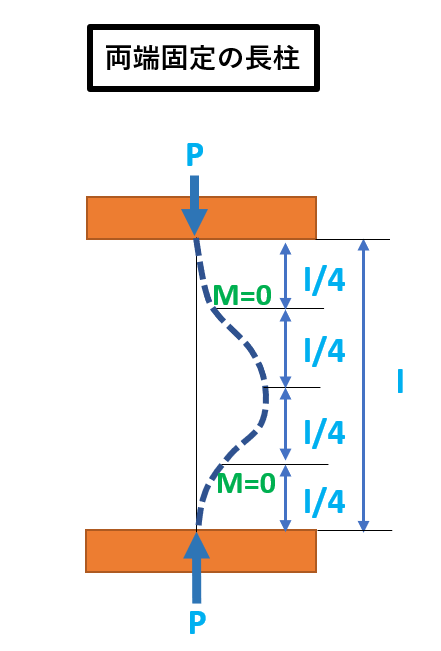
| K=4 | 両端固定 |
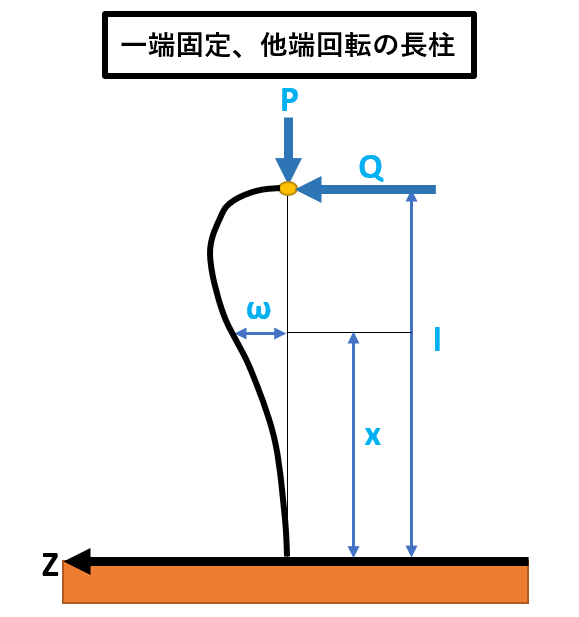
| K=2.046 | 一端固定かつ他端回転 |
座屈の種類別!オイラー座屈や座屈応力の公式
座屈の公式を以下にまとめました。
とくに他端条件により固定係数の値が変化しますので注意してください。
| 名称 | 公式 | 定義 |
| 座屈荷重(オイラーの式) | Pcr=Kπ²EI/ℓ² | E=ヤング率、I=断面二次モーメント、ℓ=長柱の長さ、K=固定係数 |
| 座屈応力 | σ=Kπ²E/λ² | K=固定係数、λ :柱の細長比(λ=ℓ/ i)、i :断面2次半径(i = √I/A)、A :柱の断面積 |
| 細長比 | λ=ℓ√(A/KI) | I=断面二次モーメント、ℓ=長柱の長さ、K=固定係数、A=断面積 |
| 許容座屈荷重 | Ps=K/S×π²EI/ℓ² | I=断面二次モーメント、ℓ=長柱の長さ、K=固定係数、S=安全率 |
また許容座屈荷重では、安全率Sが設定されることが多いです。
長柱の種類
| 名称 | 固定係数K |
| 一端固定、他端自由
|
1/4 |
| 両端回転自由
|
1 |
| 両端固定
|
4 |
| 一端固定、他端回転
|
2.046 |
座屈の計算例題にチャレンジ
それではココで、座屈に関連する例題を解いてみましょう。
ぜひやってみてください。
【例題】
地面に対して鉛直に固定した、長さ3mの鋼製の円柱があります。
その上部に総質量1,000kgの水槽がのっているとき、円柱の安全直径を求めなさい。
ただし、ヤング率Eを200GPa、安全率S=3とします。
【解答】
まずは許容座屈荷重を求めます。
公式より許容荷重は、Ps=K/S×π²EI/ℓ²
よってPs=(3.14³×200×10⁹d⁴)/(4×3×3²×64)=8.958×10⁸d⁴
dについて解くと、
d=⁴√(9.8×1×10³)/8.958×10⁸=5.75×10⁻²m=57.5mm
この場合の柱の細長比は、
λ=ℓ√A/KI=3×√(4πd/4)/(πd⁴/64)=24/d=417
座屈の種類!局部座屈や計算例・オイラー座屈公式まとめ
| 座屈の種類 | 定義 |
| 弾性座屈 | 弾性座屈とは、加える力が大きくなっても部材の特性が弾性範囲内にあって初期状態を維持すること |
| 非弾性座屈 | 非弾性座屈とは、部材の特性が弾性範囲を超えて初期状態から変化すること |
| 横座屈 | 横座屈とは、部材が曲がってねじれることにより、横方向にはらみ出すように変形すること |
| 局部座屈 | 局部座屈とは、部材の一部分が局部的に膨らんだりへこんだりすることで、薄い部材で起こる場合が多い座屈 |
| 名称 | 公式 | 定義 |
| 座屈荷重(オイラーの式) | Pcr=Kπ²EI/ℓ² | E=ヤング率、I=断面二次モーメント、ℓ=長柱の長さ、K=固定係数 |
| 座屈応力 | σ=Kπ²E/λ² | K=固定係数、λ :柱の細長比(λ=ℓ/ i)、i :断面2次半径(i = √I/A)、A :柱の断面積 |
| 細長比 | λ=ℓ√(A/KI) | I=断面二次モーメント、ℓ=長柱の長さ、K=固定係数、A=断面積 |
| 許容座屈荷重 | Ps=K/S×π²EI/ℓ² | I=断面二次モーメント、ℓ=長柱の長さ、K=固定係数、S=安全率 |
以上です。
ありがとうございました。