
波の干渉とは、それぞれの波が重なって互いに強めあい、または弱めあう現象です。
波の干渉における原理や条件をサクッと解説しましたので、ぜひご覧ください。
それではさっそく参りましょう、ラインナップは目次からどうぞ 😉
目次
波の干渉をわかりやすく!強め合う条件や公式・山と谷かんたん解説
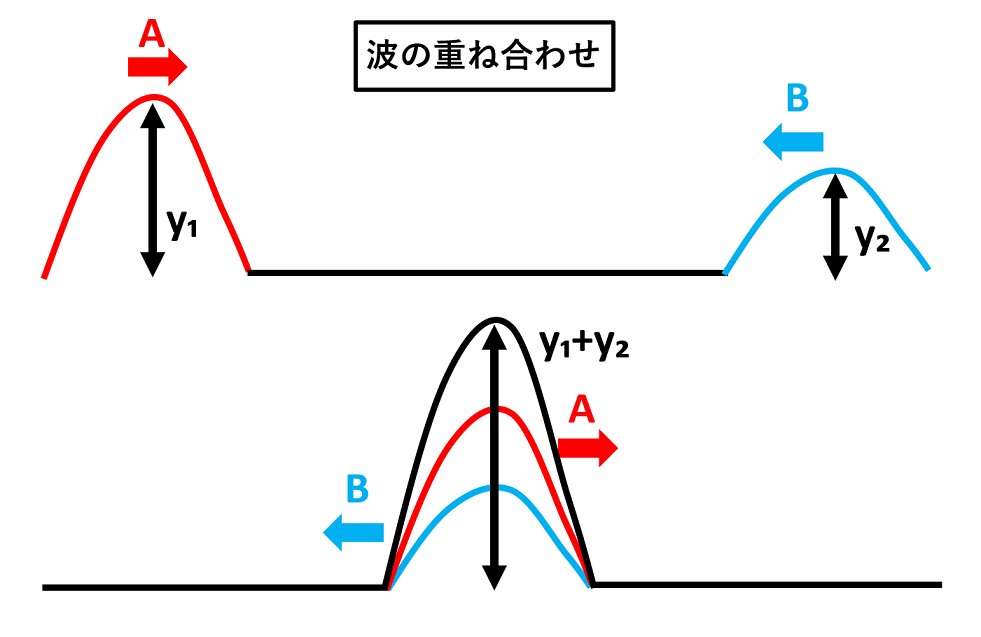
【波の重ね合わせ】
上記のように、両端からそれぞれ形のちがう波がぶつかっても、波はもとの波の形を保って進みます。
このように、2つの波がぶつかっても波の振幅や波長などは変化しません。
この性質を【波の独立性】といいます。
一方、それぞれの波がぶつかった瞬間、どちらの波形でもない別の波形ができます。
このとき、媒質の変位yはy₁とy₂を足し合わせたものとなるのです。
y=y₁+y₂
この関係を【波の重ね合わせの原理】と呼んでいます。
水面波の干渉をわかりやすく解説

2つの波の山と谷が重なった所では、2つの波が打ち消し合って振動しません。
このような部分を節線(せっせん)といいます。
節線と節線の間は、2つの波の山と山、または谷と谷が重なるところであり、それぞれの波が強めあって大きく振動します。
それでは波の強め合いと打ち消し合いの条件と公式をみていきましょう。
以下の図をご覧ください。
【2つの波の干渉(水面波)】
.png)
波の干渉➀波が強め合う条件と公式
波源S₁とS₂は同位相の波をだします。
よってS₁、S₂から等距離の地点では波の変位は等しいです。
したがって、直線S₁P上にS₁Q=S₂Pとなる点Qをとると、Q点でのS₁からの波の変位とP点でのS₂からの波の変位は同じになります。
よって、波の変位は1波長ごとに繰り返されるので、QPが波長の整数倍ならば、2つの波が強め合う条件はmを整数として以下の式が成り立ちます。
|S₁P-S₂P|=mλ
波の干渉②波が打ち消し合う・弱め合う条件と公式
2つの波が打ち消し合うのは、2つの波の変位が逆になった場合です。
変位が逆になるのは、距離にして半波長の差にあたるから、QPが波長の整数倍+半波長になっていれば、P点におけるS₁からの波とS₂からの波の変位が逆になり打ち消し合います。
よって2つの波がうち消しあう条件は、
|S₁P-S₂P|=(m+1/2)λ
となります。
それぞれの条件は、2つの波源S₁、S₂が同位相の波を送り出しているときのみ成り立ちます。
もし位相がπだけずれていたとすると、条件式も入れ替わり、|S₁P-S₂P|=mλが弱め合う条件、|S₁P-S₂P|=(m+1/2)λが強め合う条件となることを覚えておきましょう。
波の干渉の種類!定常波・進行波・反射波・入射波
干渉における波の種類は以下のとおりです。
波の種類
| 定常波 | 波長と振幅が同じ2つの波が反対方向に進み干渉したときの、左右どちらにも進まない波
入射波と反射波が干渉する場合にできる |
| 進行波 | 波長と振幅が同じ2つの波が反対方向に進み干渉したときの、移動する波 |
| 反射波 | 波動のうち、進行する波に対して逆向きに進行する波
端で反射して入射波と反対向きに戻って来る波 |
| 入射波 | 波源から発生して他端に進んでいく波 |
定常波ができているとき、媒質がいつも大きく振動する場所を【腹】といいます。
腹の振幅はもとの波の2倍です。
一方、2つの腹の間には、媒質がまったく振動しない場所があり、その部分を【節】といいます。
となり合う腹と腹の間隔はもとの波の波長1/2、となり合う腹と節の間隔はもとの波の波長1/4です。
媒体の種類によって波の形も変化
また、媒体の種類によっても波の形が変わります。
たとえば、媒質の端が自由に振動できる場合を自由端といいます。
自由端で波が反射するときは位相は変化せず、上下はそのままになります。
入射波と反射波が重なっている部分の波形は入射波と反射波の変位を合成したものとなり、最大変位は入射波の2倍です。
そして媒質の端が振動できない状態になっている場合が固定端。
固定端で波が反射するときは、位相はπだけずれ、上下が反転します。
固定端の媒質は振動できないため、変位は常に0です。
このため入射波と反射波の変位の向きが反対で大きさが等しくなっていると覚えておきましょう。
| 自由端 | 固定端 |
| 媒質の端が自由に振動できる場合
波が反射するときは位相は変化せず、上下はそのまま 入射波と反射波が重なっている部分の波形は入射波と反射波の変位を合成したものとなり、最大変位は入射波の2倍 |
媒質の端が振動できない状態になっている場合
固定端で波が反射するときは、位相はπだけずれ、上下が反転 入射波と反射波の変位の向きが反対で大きさが等しくなっている |
そのほか、波の公式や波長グラフについてはまた別記事でまとめていますので併せてご確認ください。
波の干渉をわかりやすく!強め合う条件や公式・山と谷まとめ
波の干渉や発生条件、原理などは以下のとおりです。
| 波の重ね合わせの原理 | y=y₁+y₂ |
| 波の干渉で強め合う条件 | |S₁P-S₂P|=mλ
※2つの波源S₁、S₂が同位相の波を送り出しているときのみ。πだけずれると逆になる |
| 波の干渉で打ち消し合う条件 | |S₁P-S₂P|=(m+1/2)λ
※2つの波源S₁、S₂が同位相の波を送り出しているときのみ。πだけずれると逆になる |
| 自由端(反射波の位相) | 位相変化なし |
| 固定端(反射波の位相) | 位相がπ変化する |
| 定常波 | 波長と振幅が同じ2つの波が反対方向に進み干渉したときの、左右どちらにも進まない波
入射波と反射波が干渉する場合にできる |
| 進行波 | 波長と振幅が同じ2つの波が反対方向に進み干渉したときの、移動する波 |
| 反射波 | 波動のうち、進行する波に対して逆向きに進行する波
端で反射して入射波と反対向きに戻って来る波 |
| 入射波 | 波源から発生して他端に進んでいく波 |
以上です。
ありがとうございました。
