今回のテーマはトラス構造における力の分解についてです。
計算例題も載せておきましたのでぜひチャレンジしてみてください。
目次
トラス構造の力の分解について!計算例題でサクッと解説
〈トラス構造★東京ゲートブリッジ〉

トラス構造とは、構成される三角形△を単位とした構造骨組のひとつで、各部材の端部節点がすべてピン接合となっているものを指します。

ピン接合は部材同士を一体化させずに留める接合方法で、接合部が自由に回転するため、曲げモーメントが発生しないなどのメリットがあるよ
トラス構造のメリットとデメリットを簡単にまとめるとこんな感じ 🙂
| メリット | デメリット |
| 強度が高い
軽量化が可能 細い部材で構造物を建設できる デザイン性が高い |
ある程度の高さが必要
費用が高くなる可能性が高い 組み立てに時間がかかる |
荷重がかかっても各部材には軸方向に圧縮力か引張力しか発生せず、曲げモーメントを受けにくい構造のため、強いんです!
ちなみに曲げモーメントは、曲げる力のことで、曲げモーメントが発生する箇所には、梁が曲がろうとする力が作用するため補強が必要となります。
よってトラス構造は変形しにくく強い構造とされ、ドームなどの大空間や橋の架構、大きい構造物(駅)などに使用されていますよ 😀
【例題】トラス構造!力の分解と計算方法
それでは、トラス構造の例題(力の分解)を解いてみましょう。
例題:以下の三角トラスを解き、それぞれ①~⑧材の応力を求めなさい。
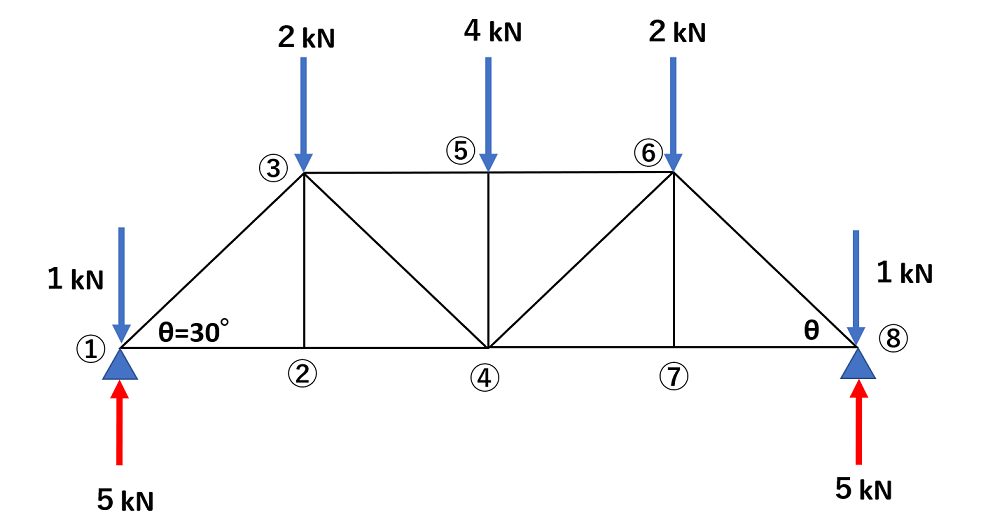
【解答】
トラス構造の問題は複雑でむずかしいですよね。
だけどひとつずつ解いていけばかならず解けるようになります。
まずは①の部分から見ていきましょう。
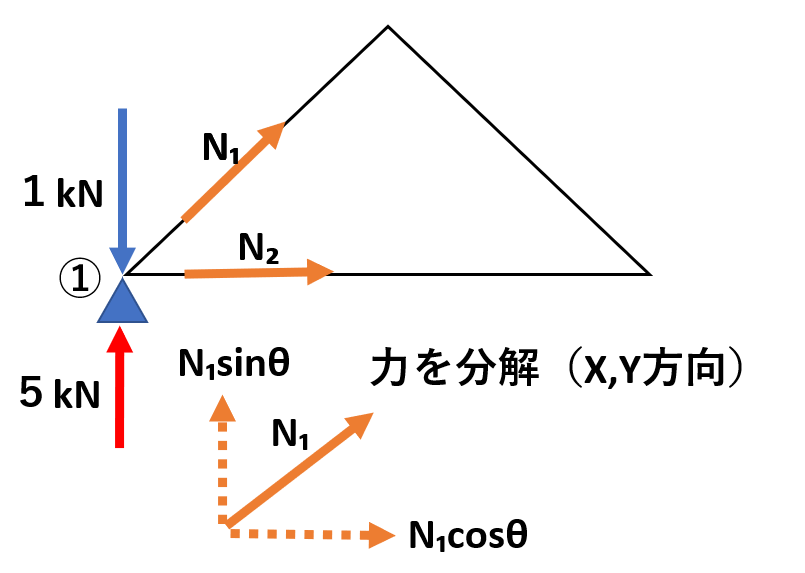
力のつり合いの式を立てるため、X,Y軸方向に合わせて力を分解します。
①に関連する材の力をN₁、N₂と仮定します。
とくにN₁は斜めになっているので、力を分解して力の向きをそろえましょう。
そうすると、以下のような式が立てられます。
①式:N₂+N₁cosθ=0
②式:1kN=5kN+N₁sinθ
また、θ=30°であるので、sinθ=1/2、cosθ=√3/2
よって
N₁=-8kN
N₂=4√3kN
つづいては②の部分です。
実は②の部分は超ラッキー部分!
荷重のかからない【T】の部分は力がゼロになります。
覚えておくと便利ですのでぜひチェックしておいてください。
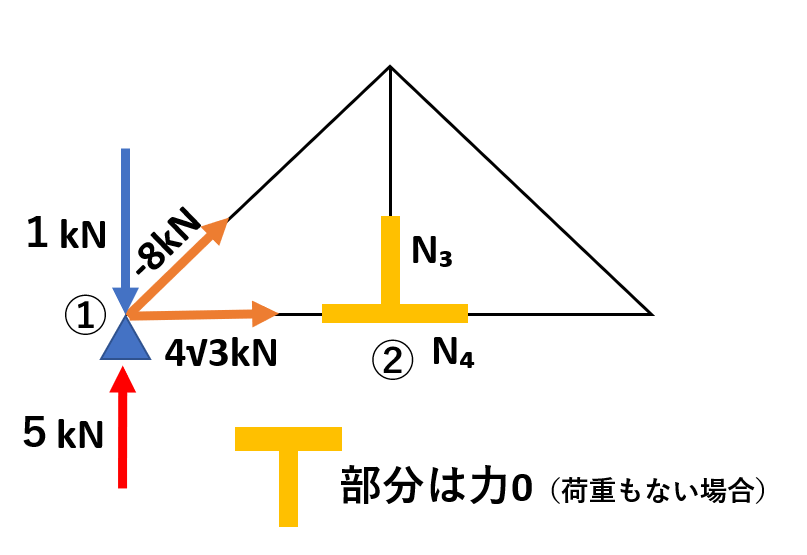
よって②部分は、
水平方向N₂=N₄=4√3kN
垂直方向N₃=0kN
となります。
同じように③以降も力を分解し解いていくと、以下の図のような力の分解となります。
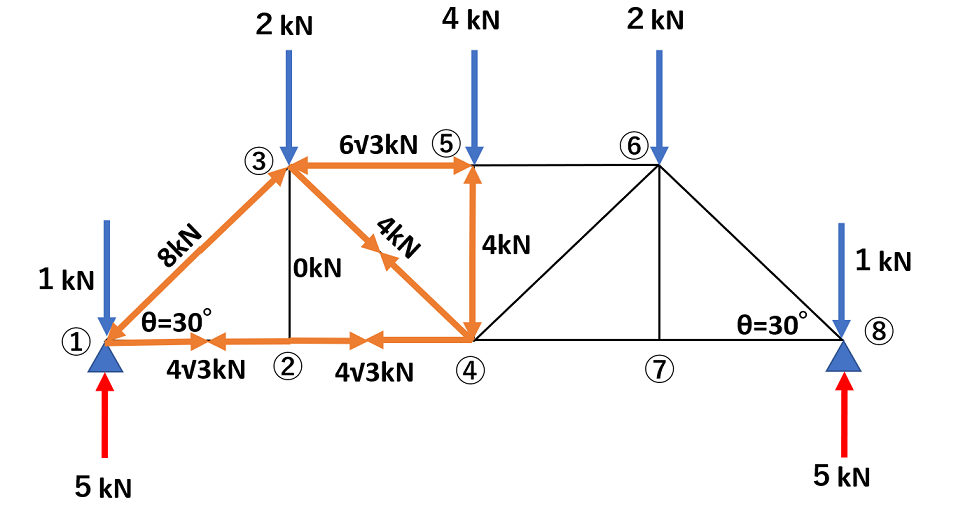
※⑤~⑧も同じ(左右対称)
改めて、トラス問題のポイントは、力のつり合いのために力を分解することと、応力がゼロの部分を見極めることです。(T部分②⑦)
このふたつを押さえながら、トラス構造の問題をくりかえし解いてみてください。
このほか応力関連で、断面係数やせん断応力の計算例題も別記事でまとめていますので、併せてご確認ください。
トラス構造の【力の分解】まとめ

ポイント
力のつり合いの式を立てるため、X,Y軸方向に合わせて力を分解する
荷重のかからない【T】の部分は力がゼロになる(荷重もない場合)
以上です。
【関連記事】
ありがとうございました。
.png)