機械分野では、流体力学として【ベルヌーイの定理】を勉強します。
基本的な考え方や公式、問題の求め方を例題で解きながらわかりやすく解説していきます。
それではさっそく参りましょう、ラインナップは目次からどうぞ 🙂
目次
ベルヌーイの定理をわかりやすく!例題で公式や問題の求め方をチェック

ベルヌーイの定理って何?わかりやすく教えて
ベルヌーイの定理とは、理想流体の定常流れにおいて、流線上でエネルギーが保存されることを示した定理とも言えるでしょう。
そして質量保存則と同じように、一般性のある法則として【エネルギー保存則】があります。
粘性や摩擦がなく、圧縮を考慮しない【理想気体】の定常流で、外力として重力だけが作用する場合に流線に沿って成り立つ【エネルギー保存則】が【ベルヌーイの定理】です。
エネルギーの種類としては、位置エネルギー、運動エネルギー、圧力エネルギーがありますが、これらの総和がどこの場所でも一定になります。
P(圧力)+(1/2)ρⅴ²(運動)+ρgh(位置)=一定
【ベルヌーイ★図解】
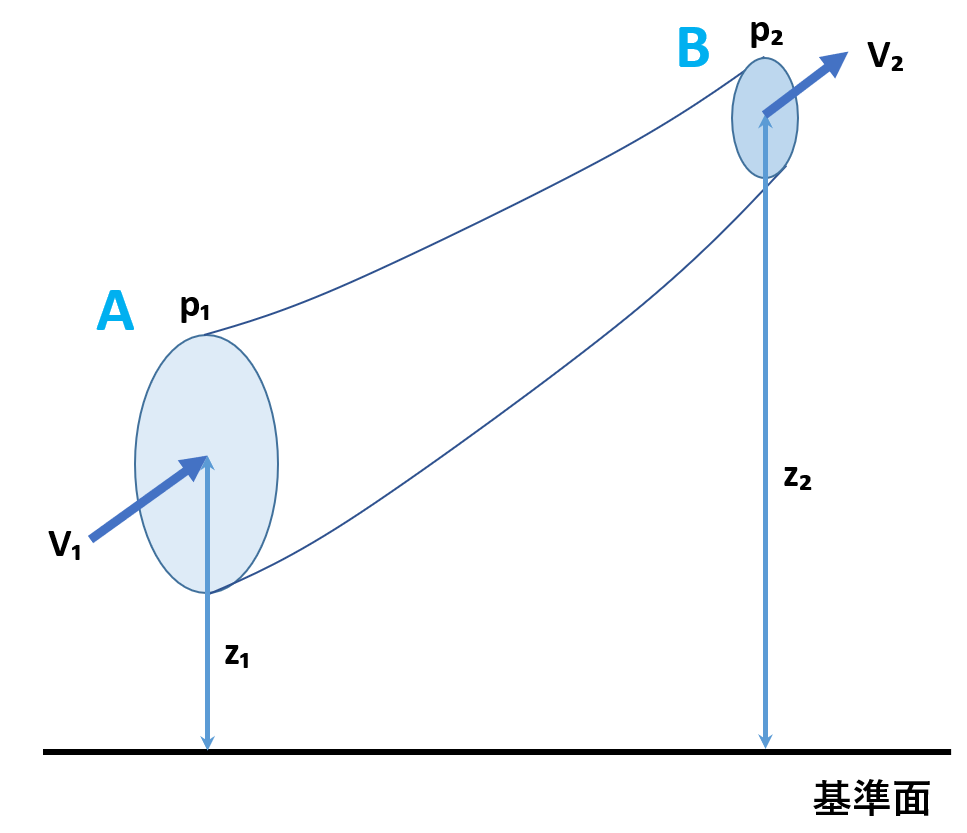
一方、上記のような流管を考えるとき、AとBの面において、mを流体の質量流量(kg/s)、それぞれの位置水頭をz₁、z₂、圧力水頭p₁、p₂、速度水頭v₁、v₂、流体の密度をρとすると、ベルヌーイの定理は以下の式で表されます。
mgz₁+mp₁/ρ+(1/2)mv²₁=mgz₂+mp₂/ρ+(1/2)mv²₂=一定…①
そして、それぞれの式に関係しているエネルギーは以下のとおりです。
| エネルギーの種類 |
| 位置エネルギー |
| 圧力エネルギー |
| 運動エネルギー |
また、①の式の各辺をmgで割ると、
z₁+p₁/ρg+v₁²/2g=z₂+p₂/ρg+v₂²/2g=一定…②
と表せます。
②の式において、zを位置水頭(位置ヘッド)、p/ρgを圧力水頭(圧力ヘッド)、v²/2gを速度水頭(速度ヘッド)とよび、その総和が全水頭(トータルヘッド)となります。

①、②の式どちらも【ベルヌーイの定理】ですので覚えておきましょう。
ベルヌーイの定理は何に使える?
例えば、位置や高さ、径が異なるパイプ管での圧力差や流速などがわかり、パイプの強度を決定するのに役立ちます。
そのほか、飛行機では揚力と関連してベルヌーイの定理が使用されており、飛行機が飛ぶ仕組みにも深く関係しています。
このように、とくに設備や機械系の分野では、上限値や仕組みをつくるための必要な定理となります。
一方で、アルキメデスの原理も設備系の調査でよく使われますので併せてチェックしてみてください。
ベルヌーイの定理の公式やわかりやすい求め方
公式は以下のとおり。
P(圧力)+(1/2)ρⅴ²(運動)+ρgh(位置)=一定
高さや圧力、速度などが違う点でも、理想流体上でエネルギー総和は一定になります。
ベルヌーイの定理の例題・練習問題!わかりやすく解説
それではココで、ベルヌーイの定理に関する例題を解いてみましょう。
ぜひチャレンジしてみてください。
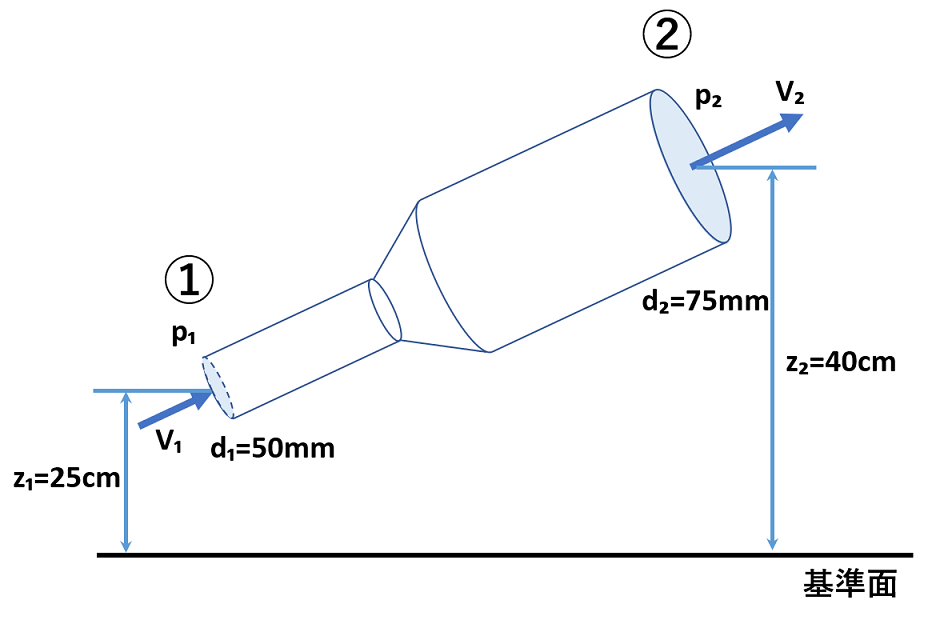
【例題】
上記の図のような傾斜のついた拡大管を水が流量Q=1200cm³/sで流れています。
点1と点2での管径は、それぞれd₁=50mm、d₂=75mm、基準面からの高さは点1がz₁=25cm、点2がz₂=40cmでした。
流れる水の密度ρ=1000kg/m³、重力加速度g=9.81m/s²として、以下の問いに答えなさい。
(1)①および②の流速v₁、v₂を求めなさい。
(2)①での圧力p₁をp₁=5000Paとして、②での圧力p₂を求めなさい。
(1)について
(2)について
物理(圧力)系の計算問題としてはボイル・シャルルの問題も別記事にまとめています。
ベルヌーイの定理をわかりやすく!例題で公式や問題の求め方まとめ
ポイント
ベルヌーイの定理とは、理想流体の定常流れにおいて、流線上でエネルギーが保存されることを示した定理
圧力エネルギー、運動エネルギー、位置エネルギーなどの種類がある。
【公式】P(圧力)+(1/2)ρⅴ²(運動)+ρgh(位置)=一定
例題を解いてベルヌーイの定理の理解を深めよう!
以上です。
ありがとうございました。
