今回のテーマは【材料力学における公式】
材料工学で出てくる公式をまとめましたので参考にしてください。
それではさっそく参りましょう、ラインナップは目次からどうぞ 🙂
目次
応力の公式一覧!材料力学(工学)やねじり応力の公式&定義をチェック
材料力学の公式をそれぞれみていきましょう。
応力とひずみの公式一覧
| 名称 | 公式 | 定義 |
| 応力 | σ=P/A | σ=応力、P=内力、A=断面積 |
| せん断応力 | τ=P/A | τ=せん断力、P=内力、A=断面積 |
| 縦ひずみ(引張ひずみ) | ε=δ/l | ε=縦ひずみ、δ=変形量(伸び)、l=長さ |
| 横ひずみ(圧縮ひずみ) | ε’=-ε’/d | ε’=横ひずみ、d=幅 |
| ポアソン比 | ν=|ε’/ε| | ν=ポアソン比
縦ひずみと横ひずみの比は材料の種類ごとに一定 |
| せん断ひずみ | γ=δ/l | γ=せん断ひずみ、δ=変形量、l=長さ |
フックの法則や公称応力の公式一覧
| 名称 | 公式 | 定義 |
| ①フックの法則 | σ=Eε | σ=垂直応力、E=ヤング率、ε=垂直ひずみ |
| ②フックの法則 | τ=Gγ | τ=せん断応力、G=せん断弾性係数、γ=せん断ひずみ |
| ③フックの法則 | P=Kεv | P=部材が一様な圧力、K=体積弾性率、εv=体積ひずみ |
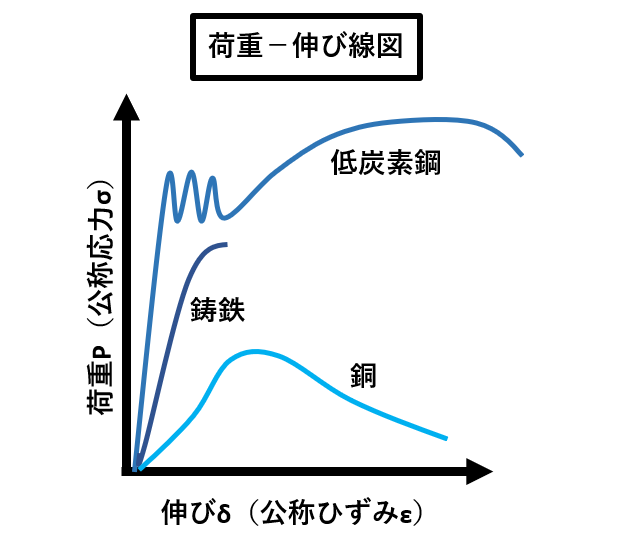
| 公称応力 | σn=P/A₀ | σn=公称応力、P=荷重、A₀=断面積(変形前)
破断における荷重Pを破断前の断面積で割ったもの |
| 公称ひずみ | εn=δ/l₀ | εn=公称ひずみ、δ=変形量(伸び)、l₀=長さ(変形前) |
| 真応力 | σt=P/A | σt=真応力、P=荷重、A=断面積
荷重が作用して物体が伸びたとき、断面積が減少することを考慮した応力 |
| ひずみ(微小増加量) | dε=dl/l | dε=ひずみ(微小増加量)、d=幅、ⅼ=長さ(標点距離) |
| 破断の伸び率 | Φ=(l’-l)/l×100% | Φ=破断の伸び率、l’=破断後の長さ、ⅼ=長さ(標点距離) |
| 破断の絞り | φ=(A-A’)/A×100% | φ=破断の絞り、A=標点間の元の断面積、A’=破断後の最小断面積 |
許容応力と安全率
| 名称 | 公式 | 定義 |
| 安全率 | S=σs/σa | S=安全率、σs=材料の基準となる強さ、σa=許容応力 |
| 許容応力 | σa=σs/S | σa=許容応力、S=安全率、σs=材料の基準となる強さ |
引張・圧縮応力の公式一覧
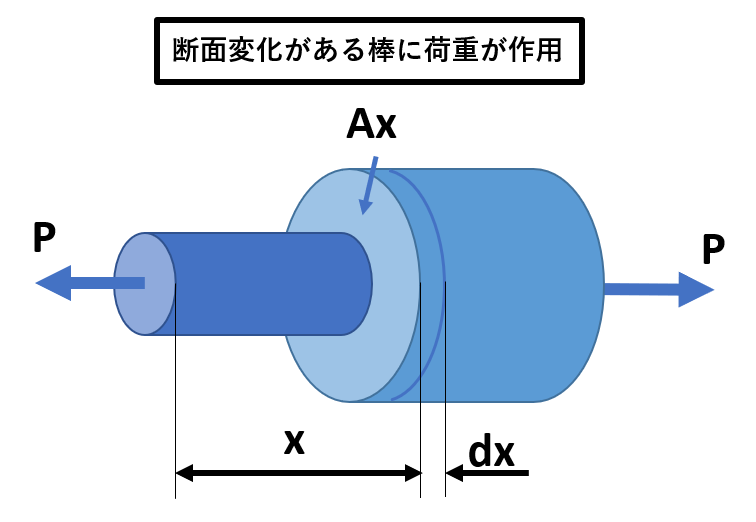
| 名称 | 公式 | 定義 |
| 微小部分の伸び(断面が変化する棒) | dδ=P/EAxdx | dδ=微小部分の伸び、P=引張または圧縮荷重、Ax=x地点における断面積 |
| 熱による伸び | δ=αⅼt | δ=熱による伸び、α=線膨張係数、ⅼ=棒材の長さ、t=上昇(下降)温度 |
| 熱応力 | σ=-Eαt | σ=熱応力、E=ヤング率、α=線膨張係数、ⅼ=棒材の長さ、t=上昇(下降)温度 |
応力についてさらに詳しく知りたい方は、また別記事で併せてご確認ください。
はりの公式一覧
| 荷重の状態
単純ばり |
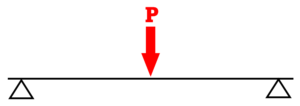
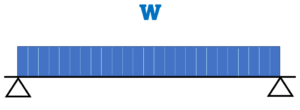
集中荷重P | 等分布荷重w |
| 端部曲げモーメント | M=0 | M=0 |
| 中央部曲げモーメント | M=P×(L/4) | M=w×(L²/8) |
| せん断力 | Q=P/2 | Q=w×L/2 |
| 変形 | δ=PL³/48EI | δ=5wL⁴/384EI |
| たわみ | θ=PL²/16EI | θ=wL³/24EI |
| 荷重の状態
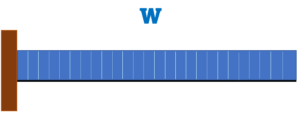
片持ちばり |
集中荷重P | 等分布荷重w |
| 端部曲げモーメント | M=P×L | M=w×(L²/2) |
| 中央部曲げモーメント | ― | ― |
| せん断力 | Q=P | Q=w×L |
| 変形 | δ=PL³/3EI | δ=wL⁴/8EI |
| たわみ | θ=PL²/2EI | θ=wL³/6EI |
| 荷重の状態
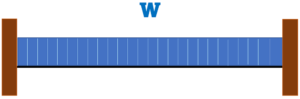
両端固定ばり |
集中荷重P | 等分布荷重w |
| 端部曲げモーメント | M=P×(L/8) | M=w×(L²/12) |
| 中央部曲げモーメント | M=P×(L/8) | M=w×(L²/12) |
| せん断力 | Q=P/2 | Q=w×L/2 |
| 変形 | δ=PL³/192EI | δ=wL⁴/384EI |
| たわみ | θ=0 | θ=0 |
ねじり応力の公式一覧や定義
| 名称 | 公式 | 定義 |
| せん断ひずみ | γ=rΦ/l | γ=せん断ひずみ、r=丸軸の中心からの位置、Φ=ねじれた角、ⅼ=丸軸の長さ |
| 比ねじれ角 | θ=Φ/l | θ=比ねじれ角、Φ=ねじれた角、ⅼ=丸軸の長さ |
| ねじり応力 | τ=Gγ=Grθ | τ=ねじり応力、G=丸棒の横弾性係数、γ=せん断ひずみ、r=丸軸の中心からの位置、θ=単位長さ当たりのねじれ角 |
| ねじり剛性 | GIp=T/θ | GIp=ねじり剛性、Ip=断面二次モーメント、T=ねじりモーメント、θ=比ねじれ角 |
| 極断面係数 | Zp=πd³/16 | Zp=極断面係数、d=幅 |
| 断面二次極モーメント | Ip=∫r²dA | Ip=断面二次極モーメント、r=半径、d=幅 |
| 動力(伝導軸) | H=Tω | H=動力(伝導軸)、T=ねじりモーメント、ω=角速度 |
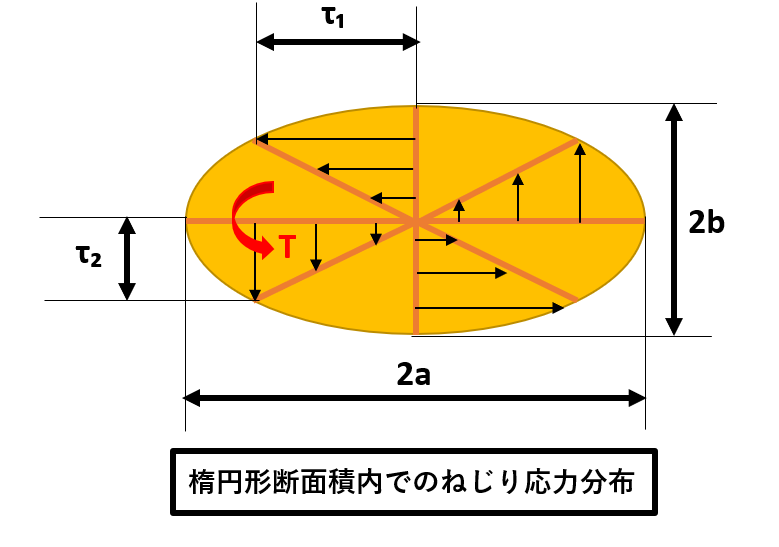
| 楕円形断面軸のねじり(最大) | τmax=2T/πab² | τmax=楕円形断面軸のねじり(最大)、τmin=楕円形断面軸のねじり(最小)、T=ねじりモーメント、a=楕円形の横幅半径、b=楕円形の縦幅半径
|
| 楕円形断面軸のねじり(最小) | τmin=2T/πa²b | |
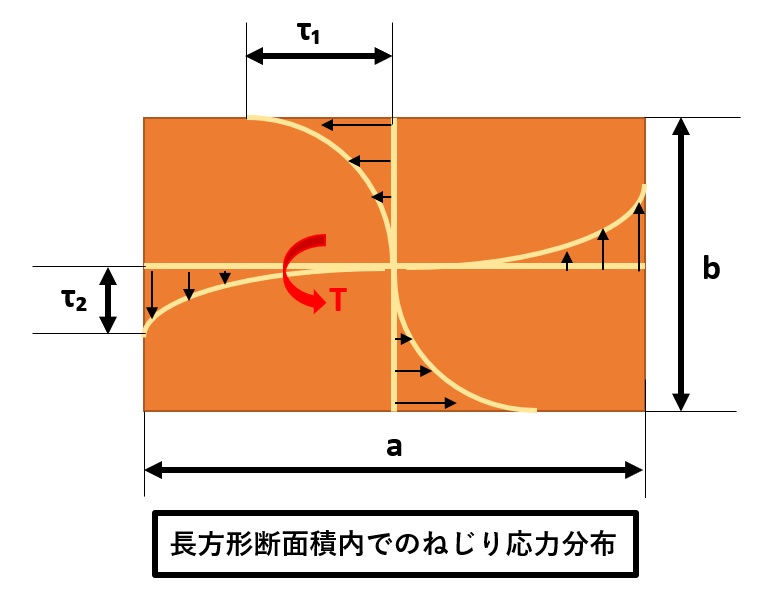
| 長方形断面軸のねじり(最大) | τmax=T/K₁ab² | τmax=長方形断面軸のねじり(最大)、τ₂=長方形断面軸のねじり(短辺に沿う)、K₁=係数(表1参照)、K₂=係数(表1参照)、T=ねじりモーメント、a=長方形の幅、b=長方形の高さ
|
| 長方形断面軸のねじり(短辺に沿う) | τ₂=K₂τmax | |
| 長方形断面軸の比ねじり角 | θ=T/K₃ab²G | θ=長方形断面軸の比ねじり角、K₃=係数(表1参照) |
表1:長方形断面軸のa/bとK₁、K₂、K₃の値
| a/b | K₁ | K₂ | K₃ |
| 1.0 | 0.208 | 1.000 | 0.141 |
| 1.25 | 0.221 | 0.916 | 0.172 |
| 1.5 | 0.231 | 0.859 | 0.196 |
| 2.0 | 0.246 | 0.795 | 0.229 |
| 3.0 | 0.267 | 0.753 | 0.263 |
| 4.0 | 0.282 | 0.745 | 0.281 |
| 5.0 | 0.290 | 0.744 | 0.290 |
| 6.0 | 0.299 | 0.743 | 0.299 |
| 8.0 | 0.307 | 0.742 | 0.307 |
| 10.0 | 0.312 | 0.742 | 0.312 |
| ∞ | 0.333 | 0.742 | 0.333 |
座屈の公式一覧
| 名称 | 公式 | 定義 |
| 長柱の座屈荷重(オイラーの式) | Pcr=Kπ²EI/ⅼ² | E=ヤング率、I=断面二次モーメント、ⅼ=長柱の長さ、K=固定係数 |
| 細長比 | λ=ⅼ√(A/KI) | I=断面二次モーメント、ⅼ=長柱の長さ、K=固定係数、A=断面積 |
| 許容座屈荷重 | Ps=K/S×π²EI/ⅼ² | I=断面二次モーメント、ⅼ=長柱の長さ、K=固定係数、S=安全率 |
長柱の種類
| 名称 | 固定係数K |
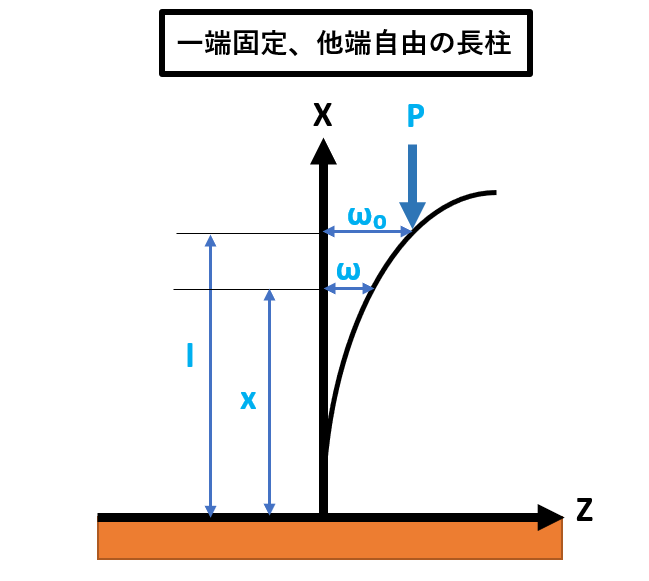
| 一端固定、他端自由
|
1/4 |
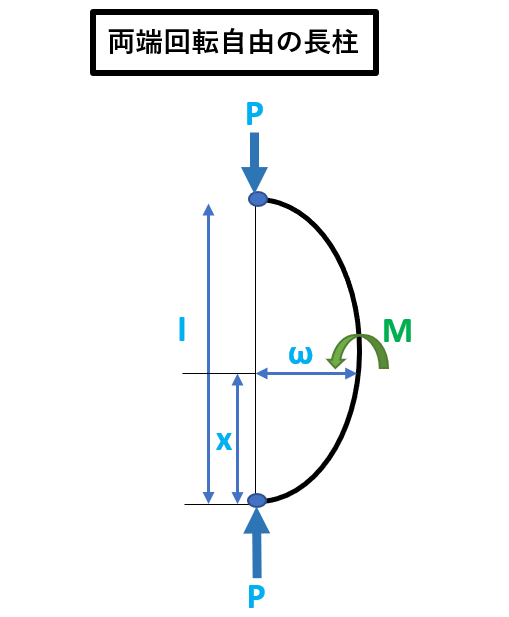
| 両端回転自由
|
1 |
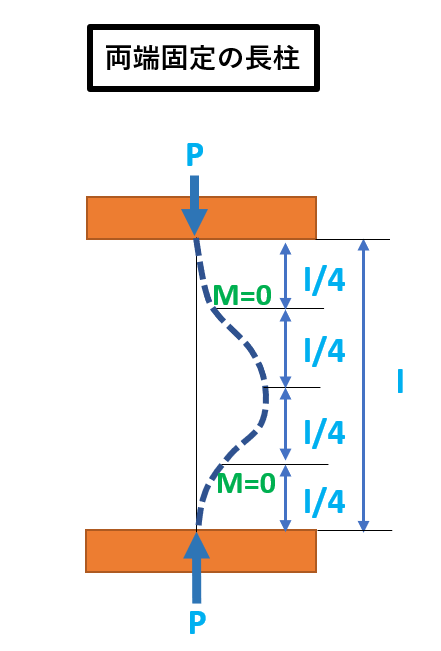
| 両端固定
|
4 |
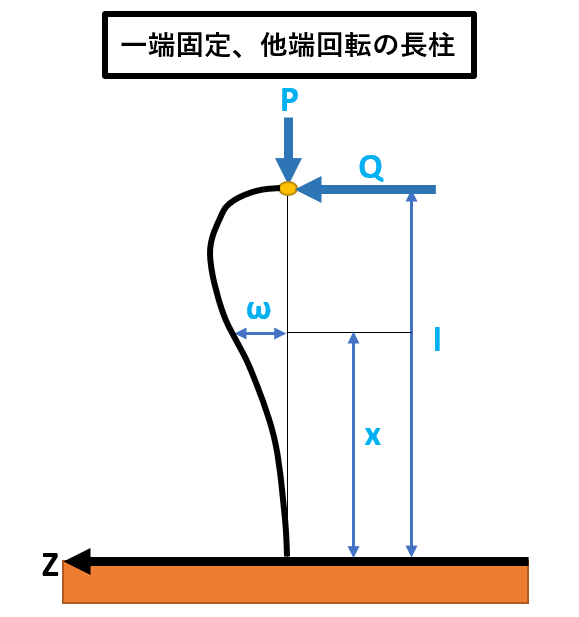
| 一端固定、他端回転
|
2.046 |
断面特性
| 断面の形 | 断面二次モーメント【Iy】 | 固定係数k² | 断面係数Z |
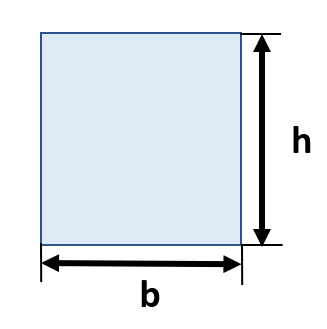 |
1/12bh³ | 1/12h²
k=0.289h |
1/6bh² |
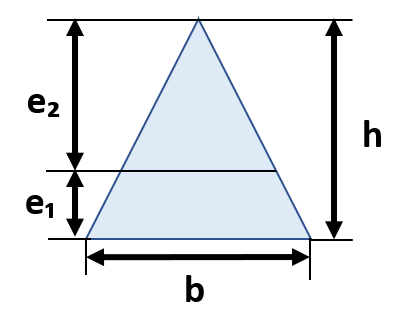 |
1/36bh³ | 1/18h²
k=0.236h |
e₁=1/3h、e₂=2/3h、Z₁=1/12bh²、Z₂=1/24bh² |
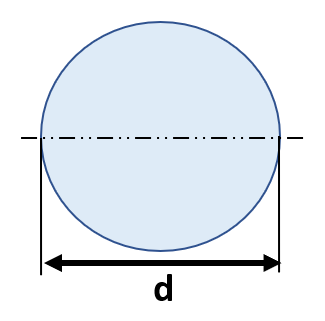 |
π/64d⁴ | 1/16d² | π/32d³ |
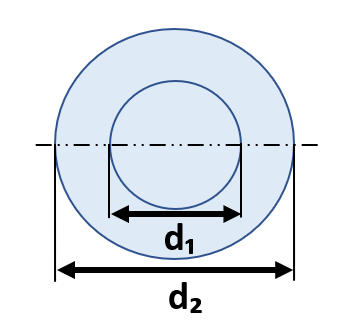 |
π(d₂⁴ーd₁⁴) | 1/16(d₂²+d₁²) | (π/32)×(d₂⁴ーd₁⁴)/d₂ |
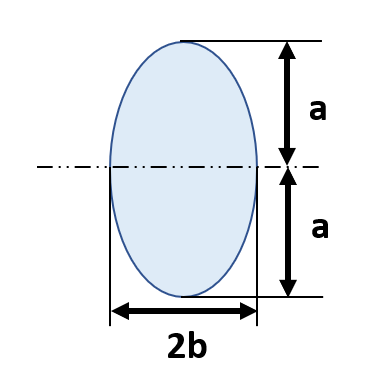 |
π/4a³b | 1/4a² | π/4a²b |
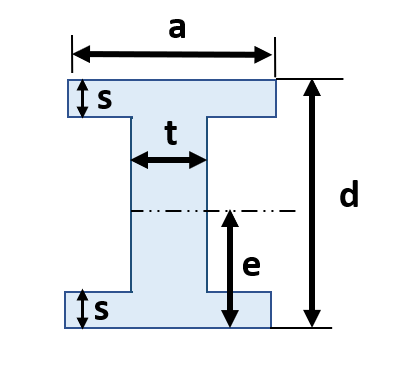 |
{ad³-h³(a-t)}/12 | {ad³-h³(a-t)}/12{ad-h(a-t)} | {ad³-h³(a-t)}/6d |
応力の公式一覧!材料力学(工学)やねじり応力の公式&定義まとめ
ポイント
材料力学一覧:図解と公式&定義をセットで確認しよう!
以上です。
ありがとうございました。