信頼度とは？計算の求め方＆直列や並列の公式もしっかりチェック

信頼度とは、ある単位時間にシステムや機械が動いている確率のことです。

そして今回のテーマは【信頼度計算の求め方】

直列や並列の公式も含めて、サクサクっと解説していきますのでぜひどうぞ！（例題付き）

それではさっそく参りましょう、ラインナップは目次からご覧ください。

信頼度の計算の求め方！公式（直列＆並列）

信頼度の計算は、直列と並列で方法が異なりますので注意してください。

信頼度の求め方！計算方法
直列 信頼度R=R₁（t）×R₂（t）×・・・×Rn（t）
並列 信頼度R=1－｛1－R₁（t）｝×｛1－R₂（t）｝×・・・×｛1－Rn（t）｝

直列のシステム信頼度の計算方法

サブシステムが直列に接続されることによって構成されているシステムです。

サブシステムとは、システムを構成する小単位のシステムのこと！

システムが正常に動作するためには、各サブシステムが”すべて”正常に動作している必要があります。

たとえば、信頼度がR₁（t）、R₂（t）・・・、Rn（t）とn個を直列に接続した場合のシステム信頼度Rは、次の式で計算できます。

信頼度R=R₁（t）×R₂（t）×・・・×Rn（t）

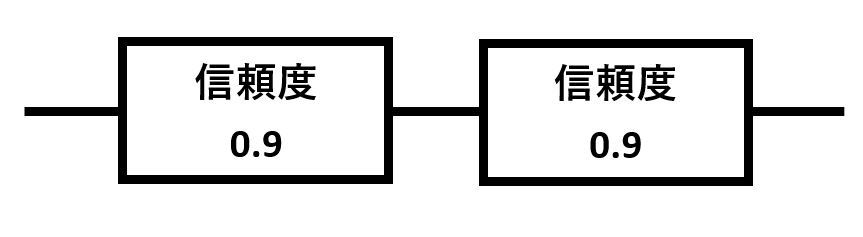
さらに具体的な数字で計算してみましょう、以下の図をご覧ください。

信頼度0.9のシステムが直列で構成されているとき、信頼度Rは

R=0.9×0.9=0.81

となります。

並列のシステム信頼度の計算方法

サブシステムが並列に接続されることによって構成されているシステムです。

並列の場合、システムが正常に動作するためには、各サブシステムのいずれかが正常に動作していればよいということになります。

このようなシステムを「冗長システム」とも呼びます。

たとえば、信頼度がR₁（t）、R₂（t）・・・、Rn（t）とn個を並列に接続した場合のシステム信頼度Rは、次の式で計算できます。

信頼度R=1－｛1－R₁（t）｝×｛1－R₂（t）｝×・・・×｛1－Rn（t）｝

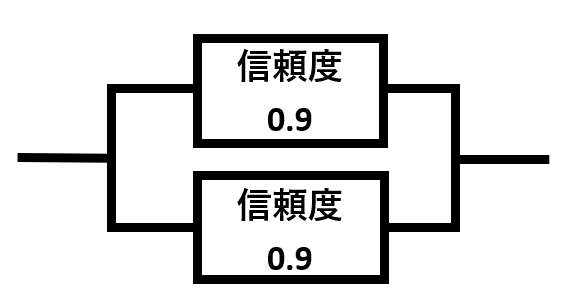
さらに具体的な数字で計算してみましょう、以下の図をご覧ください。

信頼度0.9のシステムが並列で構成されているとき、信頼度Rは

R=1－（1－0.9）×（1－0.9）=0.99

となります。

一方で、工程能力指数の計算やcpkについてはまた別記事でまとめていますので、興味のある方はぜひチェックしてみてください。

システム信頼度計算の求め方！公式を使って問題（直列・並列）を解いてみよう

【例題】

次の文章において、空欄①～③に入る最も適切なものをそれぞれ下の選択肢からひとつえらびなさい。

ただし、各選択肢を複数回もちいることはありません。

Aの信頼度：0.950

Bの信頼度：0.904

Cの信頼度：0.925

ここでシステムとしての信頼性ブロック図は以下の図1、図2が考えられます。

案1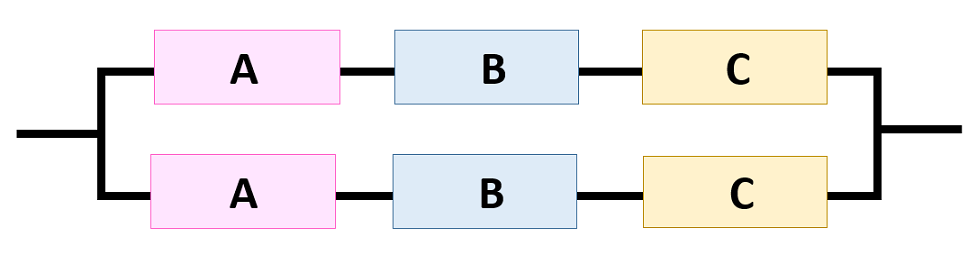
案2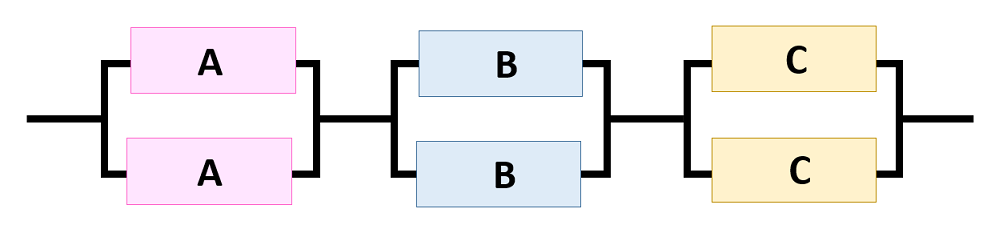

そして信頼度が高い信頼性ブロック図を採用するとしたとき、

案1の信頼度を計算すると（①）となる。

案2の信頼度を計算すると（②）となる。

よって、信頼度の高い案（③）を採用する。

【選択肢】

ア：0.983、イ：0.958、ウ：0.950、エ：0.925、オ：0.904、カ：1、キ：2

信頼度とは？計算の求め方＆直列や並列の公式まとめ

信頼度とは、ある単位時間にシステムや機械が動いている確率のこと

信頼度の求め方！計算方法
直列 信頼度R=R₁（t）×R₂（t）×・・・×Rn（t）
並列 信頼度R=1－｛1－R₁（t）｝×｛1－R₂（t）｝×・・・×｛1－Rn（t）｝

以上です。

ありがとうございました。