今回の記事テーマは【散布図と相関係数rの関係】です。
相関係数rの求め方もかんたんに解説していますのでぜひご覧ください。

それではさっそく参りましょう、ラインナップはこちらです。
目次
散布図と相関係数rの関係
散布図と相関係数r(-1~+1)の関係は、目安として以下の4つに分けられます。
| 相関 | 範囲 | 散布図 |
| つよい相関がある | r≧0.8 | 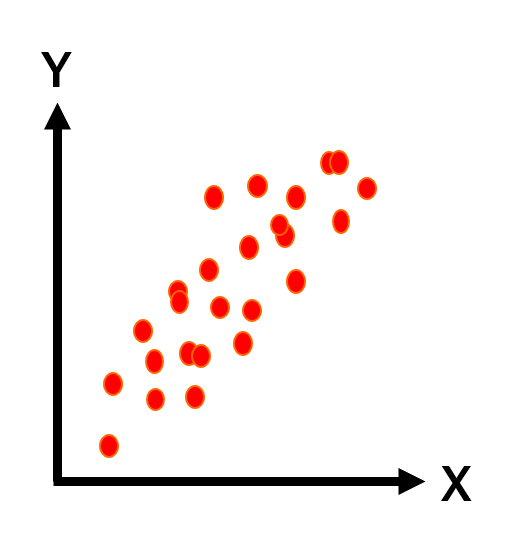 |
| 相関がある | 0.8>r≧0.6 | 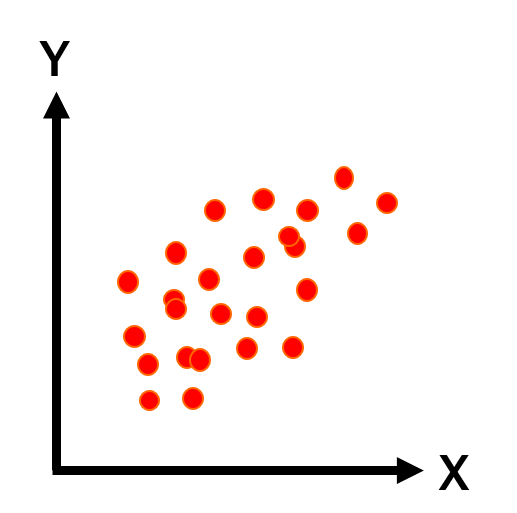 |
| よわい相関がある | 0.6>r≧0.4 | 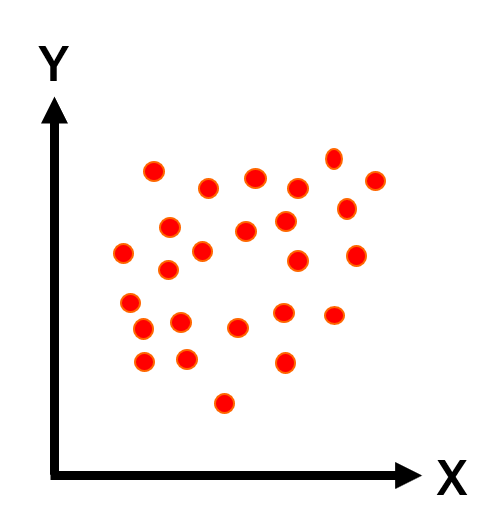 |
| ほとんど相関なし | r<0.4 | 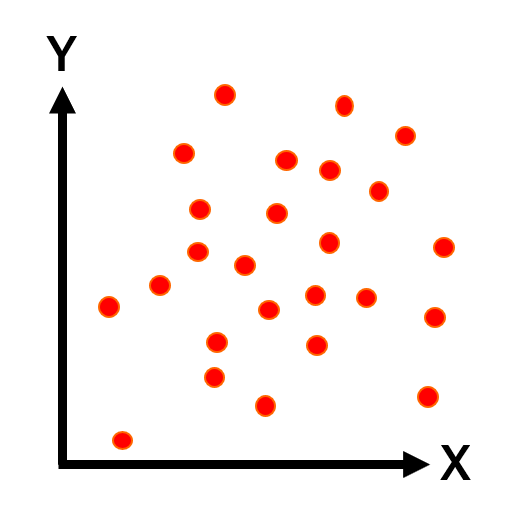 |
相関と範囲、散布図についてはセットで覚えておくと忘れにくいですよ 😉
また相関(そうかん)の意味としては、2つのものが密接にかかわっていることを表します。
相関分析とは?
相関分析とは、2つの変数間(X、Y)の関係をよりくわしく解析する方法です。

ちなみに変数が2つの場合の解析方法を【単相関分析】、3つ以上の場合は【重相関分析】といいます。
また、相関分析における散布図との関係は以下のとおりです。
| 相関 | 概要 | 散布図 |
| 正の相関 | ある変数Xが増大すればするほど、もう一方の変数Yが増大すること | 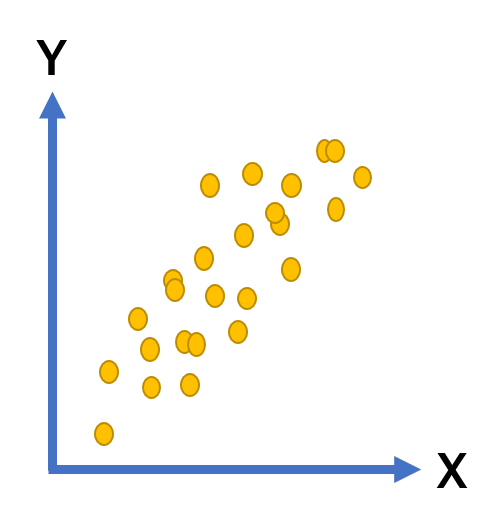 |
| 負の相関 | ある変数Xが増大すればするほど、もう一方の変数Yが減少すること | 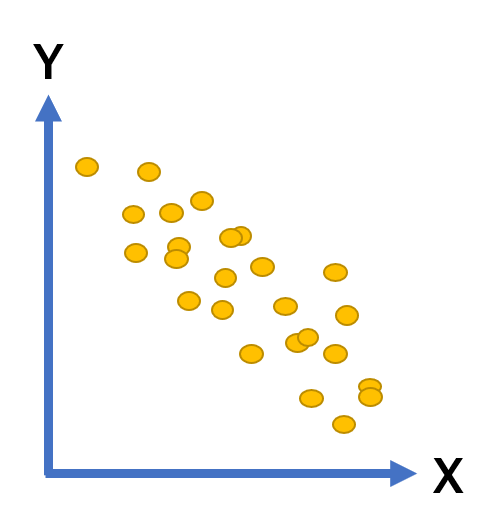 |
| 相関がない | ある変数Xが増大しても、もう一方の変数Yは無関係な値をとること | 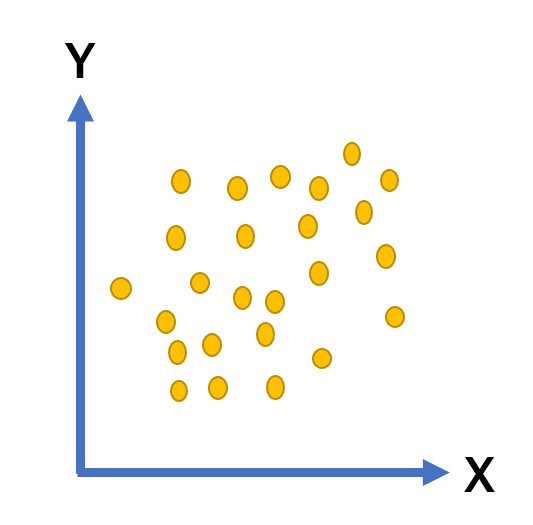 |
相関係数rとは?
相関係数rとは、2変数間にどのくらい直線的な関係があるかを示す数値で、一般的にrで表し、
範囲は【-1≦r≦+1】までのあいだの値です。
相関係数rがプラスの場合は正の相関、マイナスの場合は負の相関があることを示します。
また、相関係数rが1に近ければ相関関係が密接であることを示し、相関係数rが0に近ければ、相関関係が薄いことを示しています。

相関係数rの求め方
相関関数の公式はこちら 🙂
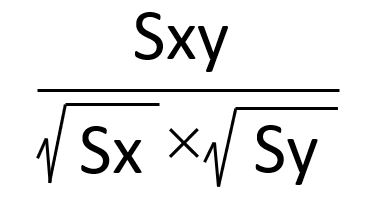
変数Xと変数Yの相関係数rを求めるために、n組のデータを用いると次のように表すことができます。
| 記号 | 意味 | 公式 |
| Sx | Xの平方和 | 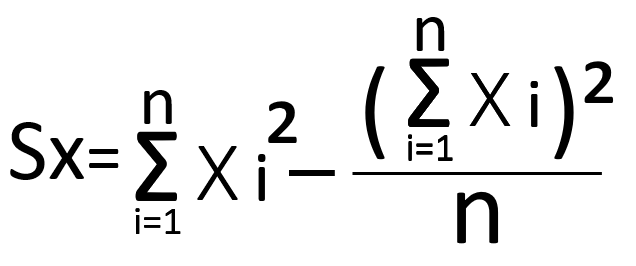 |
| Sy | Yの平方和 | 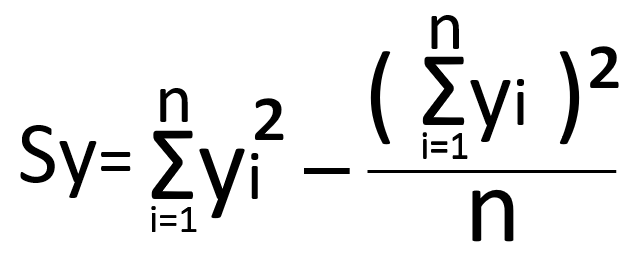 |
| Sxy | XとYの積和 | 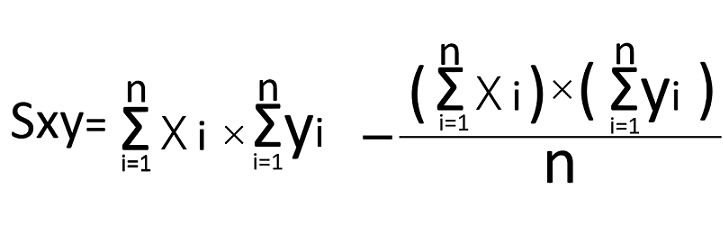 |
それではさっそく例題を解いてみましょう。
以下の表データから相関係数rを求めます。
| 変数X | 変数Y |
| 1 | 5 |
| 3 | 7 |
| 5 | 10 |
| 7 | 9 |
| 9 | 10 |
数値を整理するとこんな感じです。(n=5)
整理して表にしておくと計算ミスも防げるのでおすすめですよ 🙂
| X | Y | X² | Y² | X×Y |
| 1 | 5 | 1 | 25 | 5 |
| 3 | 7 | 9 | 49 | 21 |
| 5 | 10 | 25 | 100 | 50 |
| 7 | 9 | 49 | 81 | 63 |
| 9 | 10 | 81 | 100 | 90 |
| 計25 | 計41 | 計165 | 計355 | 計229 |
それぞれ式に当てはめて計算していくと、
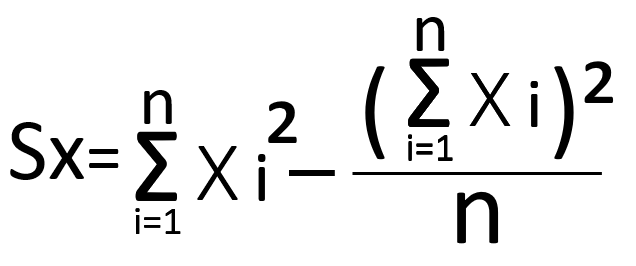 =165-(25×25)/5=40
=165-(25×25)/5=40
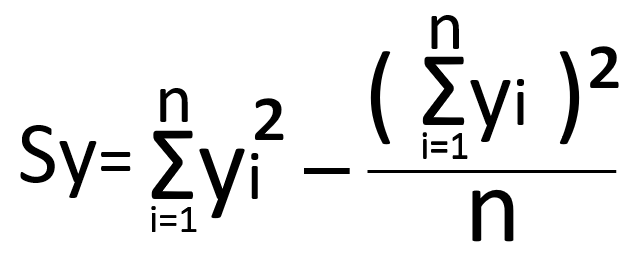 =355-(41×41)/5=18.8
=355-(41×41)/5=18.8
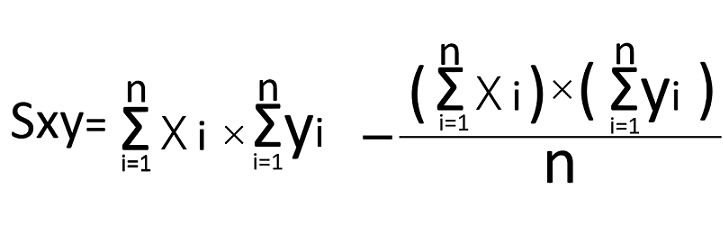 =229-(25×41)/5=24
=229-(25×41)/5=24
よって相関関数rは、
r=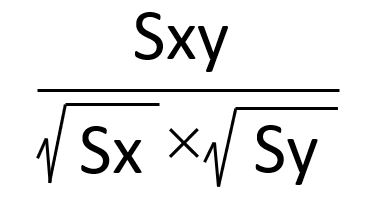 =24/(√40×√18.8)≒0.88
=24/(√40×√18.8)≒0.88
散布図と相関係数の関係まとめ
相関係数rとは2変数間にどのくらい直線的な関係があるかを示す数値で、一般的にrで表し範囲は【-1≦r≦+1】までのあいだの値
相関分析とは、2つの変数間(X、Y)の関係をよりくわしく解析する方法
散布図と相関係数rの関係【-1≦r≦1】
| 相関 | 範囲 | 散布図 |
| つよい相関がある | r≧0.8 |  |
| 相関がある | 0.8>r≧0.6 |  |
| よわい相関がある | 0.6>r≧0.4 |  |
| ほとんど相関なし | r<0.4 |  |
相関分析と散布図の関係
| 相関 | 概要 | 散布図 |
| 正の相関 | ある変数Xが増大すればするほど、もう一方の変数Yが増大すること |  |
| 負の相関 | ある変数Xが増大すればするほど、もう一方の変数Yが減少すること |  |
| 相関がない | ある変数Xが増大しても、もう一方の変数Yは無関係な値をとること |  |
相関係数の公式
| 相関係数rの求め方 | ||
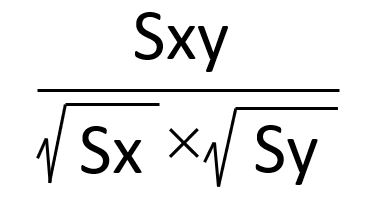 |
||
| 記号 | 意味 | 公式 |
| Sx | Xの平方和 | 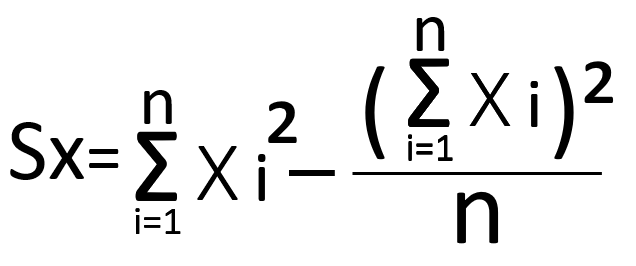 |
| Sy | Yの平方和 | 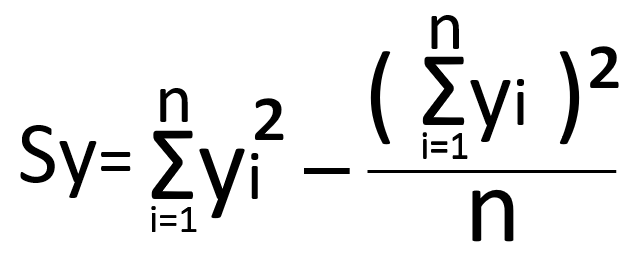 |
| Sxy | XとYの積和 | 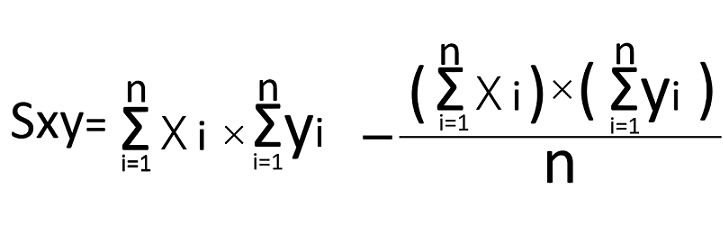 |
以上です。
また、関連記事は以下もおすすめです。
- 新qc7つ道具まとめ★覚え方や事例をわかりやすく解説
- パレート図の作り方&見方★エクセル作成法や累積比率もしっかり解説
- 管理図の種類★覚え方&見方ていねい解説【例題あり】
- 工程能力図とは?品質管理(土木)でよく使う変動データの表示法
- 正規分布とは?標準偏差との関係や見方わかりやすく解説
- ヒストグラムの作り方かんたん解説★技術系品質管理の基礎知識
興味のある方はぜひどうぞ 🙂
ありがとうございました。
