連関図法とは、
- 原因と結果
- 目的と手段
などがからみ合った問題に対し、因果化関係や要因相互の関係をとき明かし、問題を解決していく手法のこと。
特性に対して同じ要因が何回も出てくるような、要因がふくざつなときにより効果的です。
今回のテーマは言わずもがな【連関図法】
書き方や欠点、特性要因図との違いなどをわかりやすくまとめましたのでぜひどうぞ 🙂
それではさっそく参りましょう、ラインナップはこちらです。
目次
連関図法の作り方や書き方を事例でわかりやすく解説
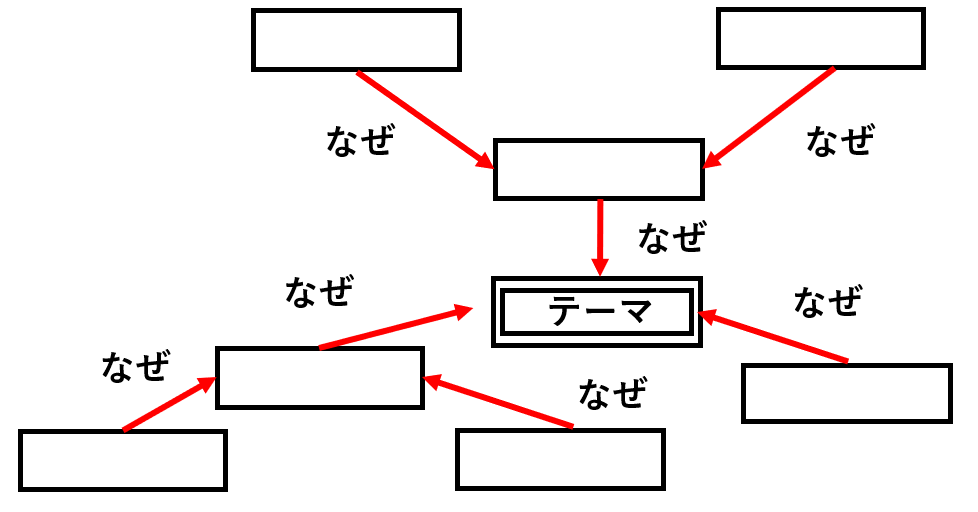
連関図法について解説していきます。
連関図法の書き方&作り方
連関図の書き方はこんな感じ 🙂
連関図の書き方
- テーマを決める(大きな紙の中央にテーマを書く)
- テーマの1次原因を考えてカード化して複数作成
- 1次原因のカードをテーマのまわりに配置して、テーマとカードを矢印でつなぐ
- 出てきた1次原因を【結果】とらえて2次原因を同じようにつくっていく
- 2次原因をカード化して関連のある1次原因カードと矢印でつなぐ
- 上記をくりかえし因果関係や要因相互の関係を明らかにする
連関図法の事例
そして連関図法がよく使われるのが【テーマ(課題)と原因(要因)】
事例としては以下のようなものが挙げられます。
| テーマ(事例) | 原因(事例) |
| なぜ売り上げがあがらないのか |
|
| なぜ図書館の利用者が増えないのか |
|
| なぜ自動車死亡事故がへらないのか |
|
何かの問題に対して

をくりかえして課題を解決していく感じですね。
ちなみに連関図は新QC七つ道具のひとつですので、他の図法も併せてチェックしておくとよいでしょう。
連関図法の利点・メリット&欠点・デメリットとは?
連関図法の利点と欠点は以下のとおりです。
| 利点(メリット) | 欠点(デメリット) |
| ①原因同士の意外なつながりから発想の転換が可能
②他の原因と関連がつよい【原因】がわかる ③課題の解決策を客観的・論理的に導き出し、その結果を現場で共有できる ④数値データを使う定量分析ではないため、統計のような専門知識も必要ない |
①人により発想のかたよりが出る可能性
②テーマに対する原因の重要性(優先順位)は分からない
|
連関図法は原因同士の意外なつながりから、さまざまな発想転換が可能です。
また数値的な定量分析ではないため専門知識も必要ないですし、課題の解決策をその場で共有できることもメリットと言えます。
逆にデメリットとしては、連関図法をつくるときに人によって発想のかたよりが出る可能性があります。
さらにテーマに対してさまざまな要因を洗い出すことができますが、原因の重要性や優先順位まではわかりません。
連関図法と特性要因図の違いをわかりやすく解説
連関図と特性要因図のちがいはこんな感じです。
| 連関図 | 特性要因図 |
 |
 |
| テーマに対して要因が円状に広がっていく構造
要因が複雑にからみ合っている場合に有効 物事の因果関係が直感的に分かりづらい |
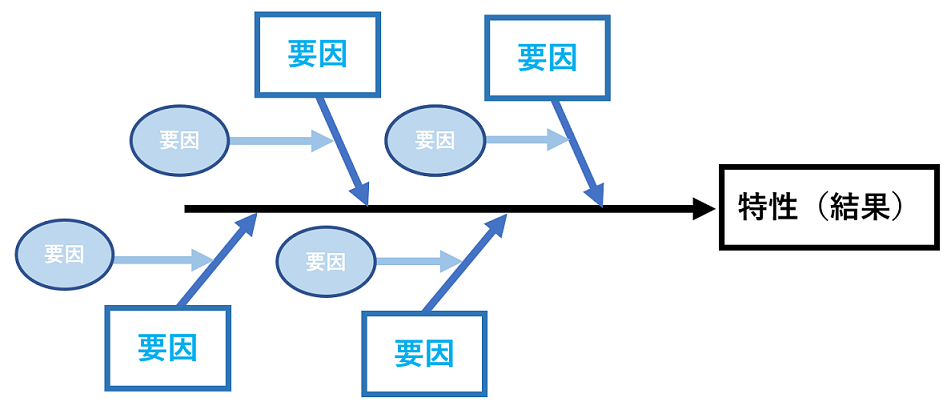
それぞれの要因が結果に向かって一直線に伸びる構造
物事の因果関係が直感的にわかりやすく、抽象的な問題も具体化して考えることができる 要因同士の因果関係を表現できない |
連関図はテーマ(課題)対して原因が円状に広がっていきます。
パっと見は複雑ですが、要因同士の因果関係も把握できるのがメリットです。
いっぽうで特性要因図は、それぞれの要因が結果に向かって一直線に伸びる構造で直感的にわかりやすいですが、要因同士の因果関係を表現できません。

連関図法の作り方や書き方をわかりやすく!特性要因図との違いまとめ
連関図法とは、【原因と結果】【目的と手段】などがからみ合った問題に対し、因果化関係や要因相互の関係をとき明かし、問題を解決していく手法
連関図法の書き方
- テーマを決める(大きな紙の中央にテーマを書く)
- テーマの1次原因を考えてカード化して複数作成
- 1次原因のカードをテーマのまわりに配置して、テーマとカードを矢印でつなぐ
- 出てきた1次原因を【結果】とらえて2次原因を同じようにつくっていく
- 2次原因をカード化して関連のある1次原因カードと矢印でつなぐ
- 上記をくりかえし因果関係や要因相互の関係を明らかにする
連関図法のメリット&デメリット
| 利点(メリット) | 欠点(デメリット) |
| ①原因同士の意外なつながりから発想の転換が可能
②他の原因と関連がつよい【原因】がわかる ③課題の解決策を客観的・論理的に導き出し、その結果を現場で共有できる ④数値データを使う定量分析ではないため、統計のような専門知識も必要ない |
①人により発想のかたよりが出る可能性
②テーマに対する原因の重要性(優先順位)は分からない
|
連関図法と特性要因図のちがい
| 連関図 | 特性要因図 |
 |
 |
| テーマに対して要因が円状に広がっていく構造
要因が複雑にからみ合っている場合に有効 物事の因果関係が直感的に分かりづらい |
それぞれの要因が結果に向かって一直線(魚のホネ)に伸びる構造
物事の因果関係が直感的にわかりやすく、抽象的な問題も具体化して考えることができる 要因同士の因果関係を表現できない |
以上です。
ありがとうございました。