今回のテーマは【ヒストグラムの上限値&下限値(データ間の決め方)】です。
ヒストグラムとは、データの分布状態や特性値、規格値の関係を表したもの。
技術系(土木・機械・電気など)の品質管理や工程管理によく使われます。

この記事はヒストグラムの上限値&下限値(データ間の決め方)、作り方や計算方法、一般的なヒストグラムの型を一覧表にまとめていますので参考にしてください。
それではさっそく参りましょう、ラインナップはもくじからどうぞ 🙂
目次
ヒストグラムの上限値&下限値とデータ間の決め方!書き方&作り方解説
ヒストグラムの作り方は以下の手順です。
ヒストグラムの作り方
- データ(サンプル数)をできるだけ多くあつめ、データの中から最大値・最小値を求め、全体の範囲を決める
- 範囲が決まったら、これをクラス分けするための幅を決める(建設工事の場合、クラス数は5~10が標準)
- 任意で幅を決めたら、この幅にもとづき度数表をつくって、それぞれのクラスに入るデータを集計していく
- 各クラスの度数が集計できたら、横軸に品質特性値、縦軸に度数を柱状に書き、ヒストグラムを作る
- さいごに規格値(上限値・下限値)を記入し、分布の状態を判定する
ヒストグラムの度数表の例
| クラス
番号 |
クラス
幅 |
代表値 | 度数 | 合計 |
| 1 | 269~272 | 270.5 | 0 | |
| 2 | 272~275 | 273.5 | 正、正 | 10 |
| 3 | 275~278 | 276.5 | 正、正、正 | 15 |
| 4 | 278~281 | 279.5 | 正、正、正、正、正 | 25 |
| 5 | 281~284 | 282.5 | 正、正、正、正、正、正 | 30 |
| 6 | 284~287 | 285.5 | 正、正、正、正、正、正、一 | 31 |
| 7 | 287~290 | 288.5 | 正、正、正、正、正、T | 27 |
| 8 | 290~293 | 291.5 | 正、正、正 | 15 |
| 9 | 293~296 | 294.5 | 正、正、T | 12 |
| 10 | 296~299 | 297.5 | 0 |

ちなみにエクセルでヒストグラムを作りたいときは、代表値をX軸、合計値をY軸にして縦棒グラフを使えばつくることが可能です。
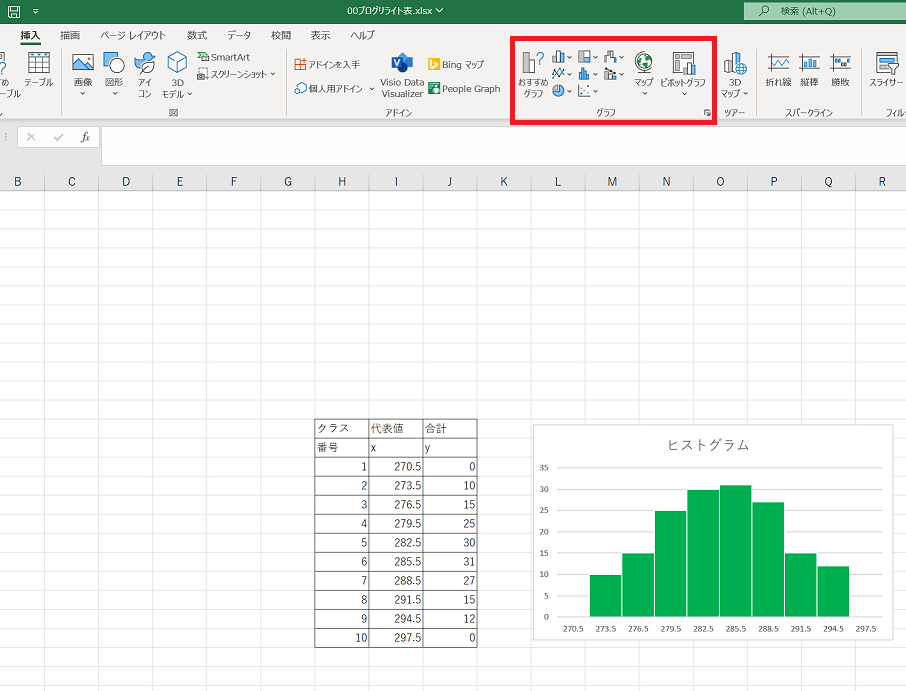
上記のエクセル表のように、①クラス②代表値③合計値を表にし、挿入のタブにあるグラフを選びましょう。
おすすめグラフではサクッとグラフをつくってくれるので簡単ですよ 🙂
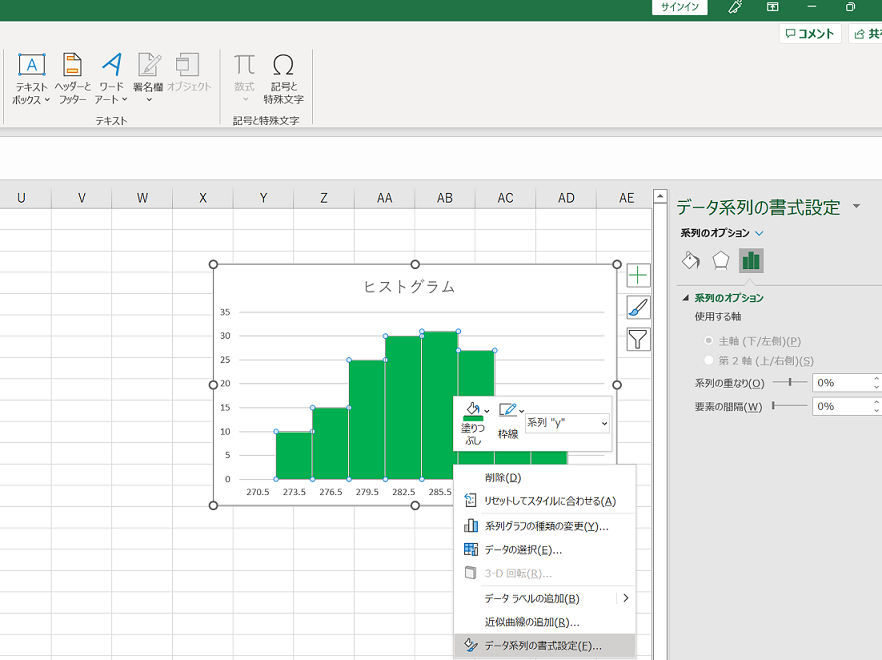
また棒の太さや色などは、右クリック【データ系列の書式設定】から変更可能です。

ヒストグラムの上限値&下限値とデータ間の決め方
たとえばデータの最大値が299、最小値が269とすると、範囲は299-269=30です。
そしてその範囲を10クラスに分けるとすると、1クラスの幅は30/10=3になります。
また、データのバラツキ幅の表し方として、以下の用語はよく出てくるのでチェックしておいてください。
| ヒストグラム
よく出る用語 |
意味 |
| 範囲(R:レンジ) | 測定値の最大値と最小値の差
例)たとえば測定値が3、4、6、7、10のとき、 R=10-3=7 |
| 平方和(S:残差平方和) | 個々のデータ平均値と各データとの差を二乗したものの和
例)S=(10-6)²+(7-6)²+(6-6)²+(4-6)²+(3-6)²=30 |
| 分散(s²) | データ個別あたりのバラツキの程度を求めることができる
残差平方和Sをサンプル数nで割ったもの 例)s²=30÷5=6 |
| 普遍分散(V) | 残差平方和Sを(n-1)で割ったもの
例)V=30÷(5-1)=7.5 |
| 標準偏差(σ) | 普遍分散の正の平方根
データのバラツキを知るためにもっともよく使われる 例)σ=√7.5=2.74 |
| 変動係数(v) | 標準偏差を平均値で割ったもの
一般的にパーセンテージ(%)で表す 例)2.74÷6×100=45.6% |
ヒストグラムの書き方
データがまとまって整理ができたら、ヒストグラムを書いていきましょう。
度数表によって集計されたデータ数を柱状に表します。
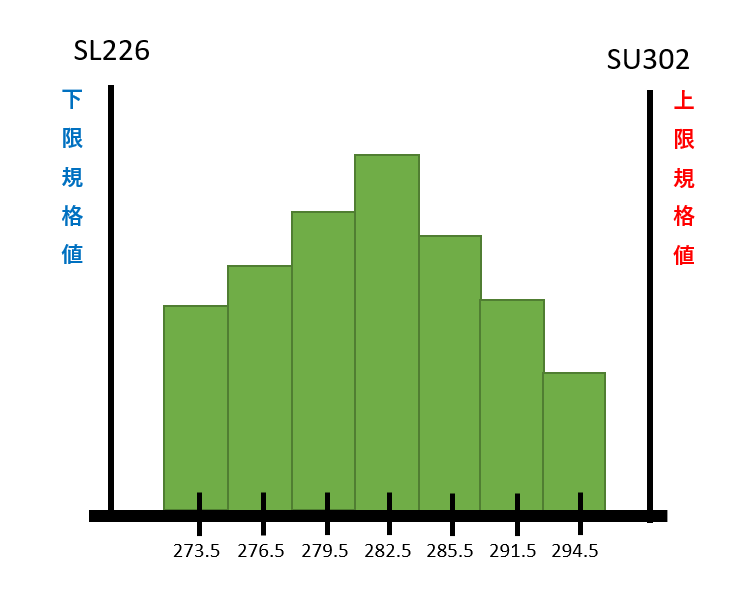
ヒストグラムを書くときの注意点はこんな感じ 😀
- 規格値を満足しているかどうか
- 分布の位置は適当か
- 分布の幅はどうか
- はなれ島のように飛びはなれたデータはないか
- 分布の山が2つ以上ないか
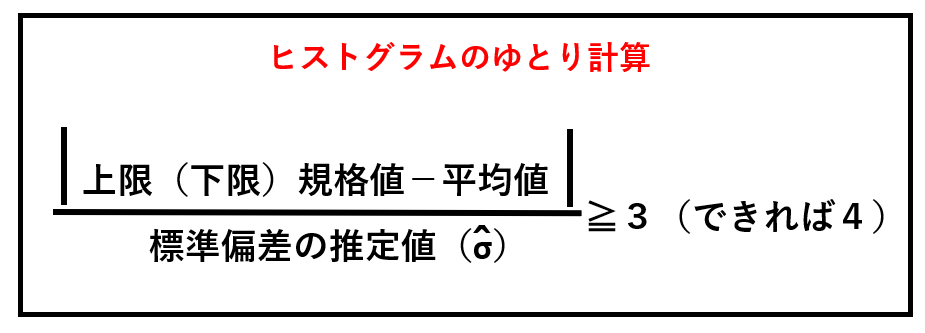
ちなみに、ヒストグラムのゆとり計算というものがあります。
以下の式を満たしていれば、規格値にゆとりがあると判定できますよ。
式 Ι 上限(下限)規格値-平均値 Ι ÷ 標準偏差の推定値(σ)≧3(できれば4)
さらにデータの区間数と区間幅を設定しましょう。
データの区間数とは、データの最大値から最小値が含まれた区間を何等分にするかということ。
区間数はデータの数により変化しますが、概略の目安はデータ数が100ぐらいまでは5~7程度、それ以上のデータであれば10程度、数千になれば15~20程度です。
データの区間幅は、データの最大値と最小値の差を区間数で割って求めます。
最小値側の境界線は、最小値から測定単位の半分を引き、これにデータの区間幅を加えると最大値側の境界線が求まります。
同じように、区間幅を順次加算すると、すべての区間幅が設定できます。
ヒストグラムの見方!一覧表
ヒストグラムの棒グラフの違いや形状で、品質管理や工程管理での意味合いが変わってきます。
一般的なヒストグラムの型を以下に一覧表にしましたので、ぜひ参考にしてださい。
| ヒストグラムの形状 | 品質管理や工程管理の一般的な関係 |
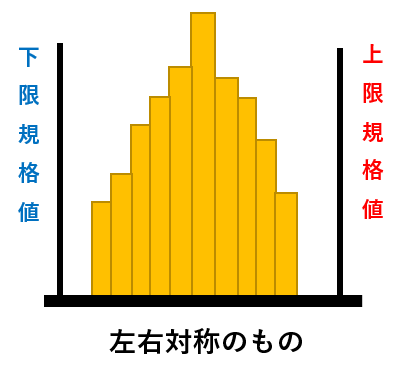 |
規格値に対するばらつきもよくゆとりもある
平均値も規格値の中心と一致する品質管理上もっとも理想的な型 |
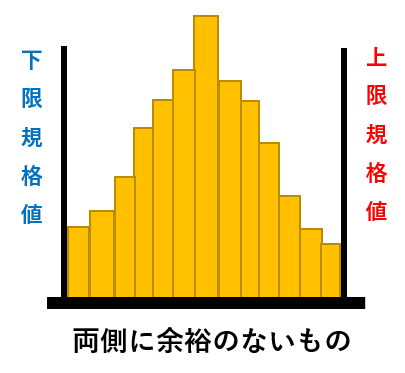 |
規格値の範囲内であるが、わずかな工程の変化によって規格値を割るものがでてしまう可能性がある
バラツキをもっと小さくするように品質管理をする必要あり |
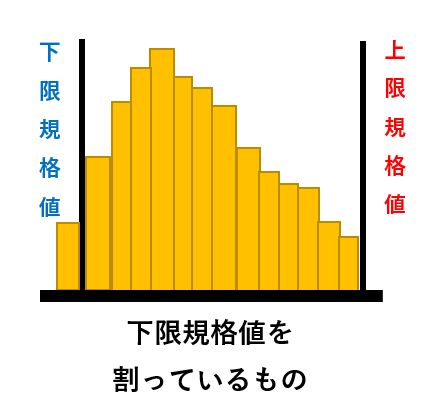 |
分布全体が左に寄りすぎ、下限値の規格値を割っている
平均値を大きいほうにずらし、バラツキを小さくするよう処置する必要あり |
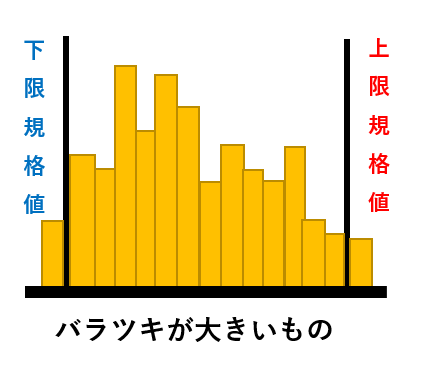 |
上・下限の規格値ともに割っており、応急処置が必要
バラツキを小さくするための要因(技術レベルや作業標準)を解析し、根本的な対策をとる必要がある |
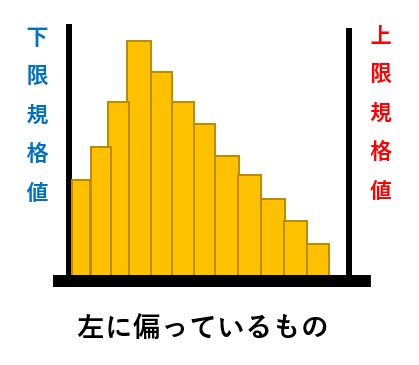 |
上限が規格値などで抑えられた場合で、特定の値以上の値をとることが許されない場合によく表れる形状 |
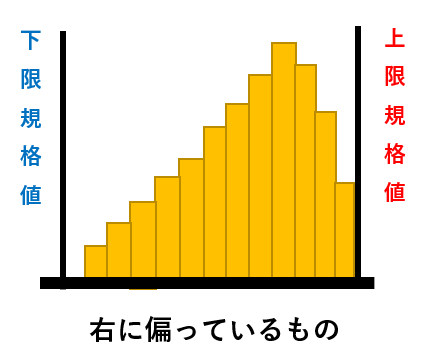 |
下限が規格値などで抑えられた場合で、特定の値以下の値をとることが許されない場合によく表れる形状 |
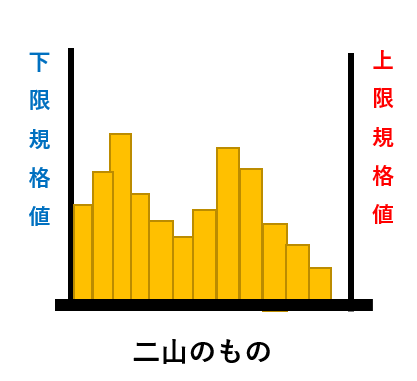 |
1つの製品の製作に2つの異なる工程を用いた場合に表れやすい分布
平均値の異なる2つの分布が混在しているもの 例)2台の機械や2種類の原材料を使用した場合など |
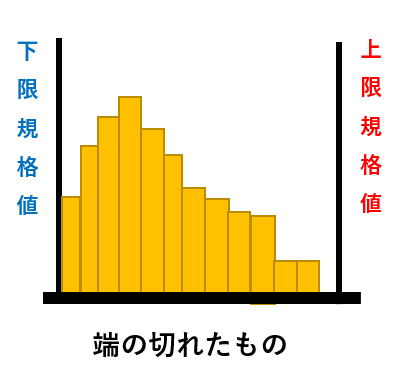 |
規格値以下のものを工程の途中で全数取りのぞいた場合に表れる型 |
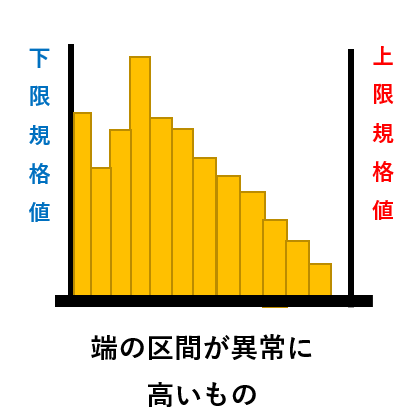 |
規格値以下のものを手直ししたり、データを偽って報告した場合に表れる型 |
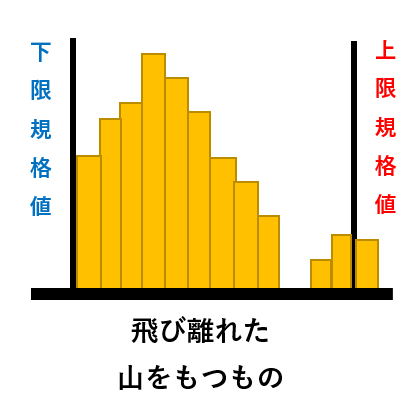 |
測定に誤りがあったり、工程に異常があった場合に表れる型 |
ヒストグラムの上限値&下限値とデータ間の決め方!書き方&作り方解説まとめ
データの区間幅(上限値&下限値)は、データの最大値と最小値の差を区間数で割って求める
ヒストグラムの作り方
- データ(サンプル数)をできるだけ多くあつめ、データの中から最大値・最小値を求め、全体の範囲を決める
- 範囲が決まったら、これをクラス分けするための幅を決める(建設工事の場合、クラス数は5~10が標準)
- 任意で幅を決めたら、この幅にもとづき度数表をつくって、それぞれのクラスに入るデータを集計していく
- 各クラスの度数が集計できたら、横軸に品質特性値、縦軸に度数を柱状に書き、ヒストグラムを作る
- さいごに規格値(上限値・下限値)を記入し、分布の状態を判定する
以上です。
ありがとうございました。