例題付きでわかりやすく解説していきますので、ぜひチャレンジしてみてください。
それではさっそく参りましょう、ラインナップは目次からどうぞ!
目次
エンタルピーをわかりやすく解説!比エンタルピーの意味や熱力学の例題
エンタルピーとは空気が持つ熱量(エネルギー)のことで、内部エネルギーと膨張・収縮するためのエネルギーを合わせたものです。
と言っても小難しいので、例題を解きながら見ていきましょう。
エンタルピーが関連する熱力学の第一法則の定義は以下のとおり。
「熱と仕事は本質的に同種のエネルギーであり、それらは互いに変換可能である。」
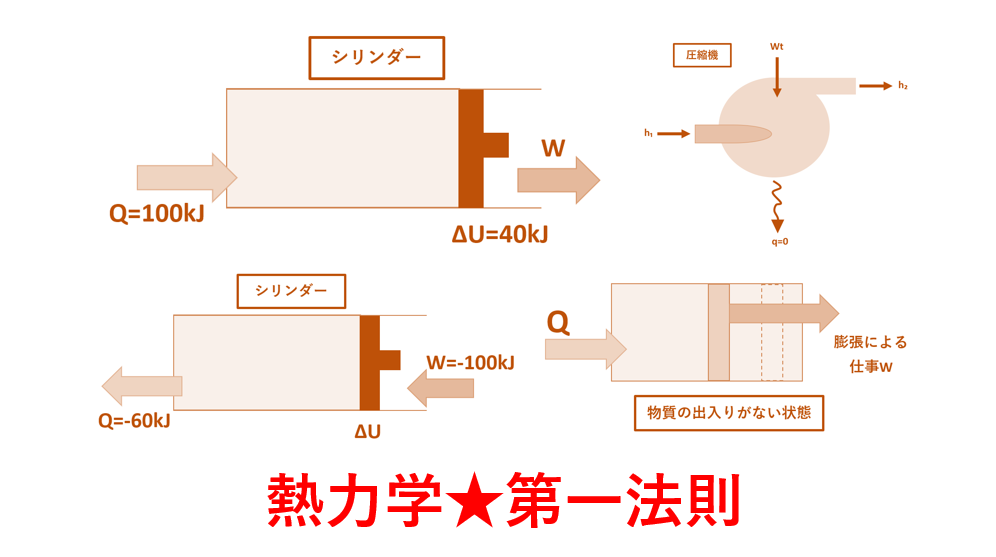
そして、シリンダーとピストンで囲まれた空間内の気体のように、物質の出入りがない状態を「閉じた系」、水車やタービンのように物質の出入りがある系を「開いた系」と言います。
閉じた系のエネルギー式をわかりやすく解説
熱力学の第一法則で、閉じた系のエネルギー式は、
Q-W=U₂-U₁
Q=(U₂-U₁)+W
※(U₂-U₁)はΔUとも表すことがある。
となります。
この式は、物体がもつ熱エネルギー(内部エネルギー)をUとしています。
そして外から物質に熱量Qが加えられ、外に仕事Wが取りだされた結果、物質の内部エネルギーがU₁からU₂に変化したことを表した式です。
ちなみに±の話ですが、Qは系外から物質に熱が加えられるときに正、Wは物質から系外に仕事が取りだされるときに正となりますので注意してください。
例題(閉じた系のエネルギー式)
ここで例題を解いてみましょう。
【例題】
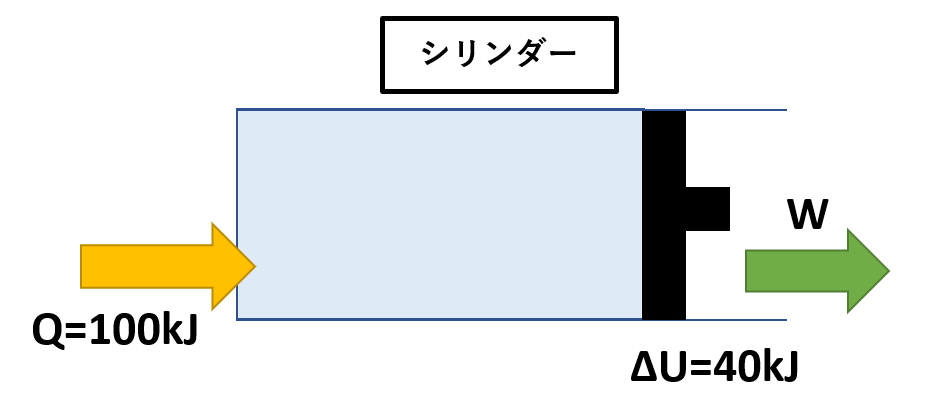
シリンダ―内部に気体が入っており、ピストンにより封じ込められているとします。次の問いに答えなさい。
(1)シリンダー外部から加熱量Q=100kJで加熱を行ったところ、気体の内部エネルギーが上昇し、内部エネルギーの変化量はΔU=40kJであった。気体がピストンに対して行った仕事量はいくらになるか。
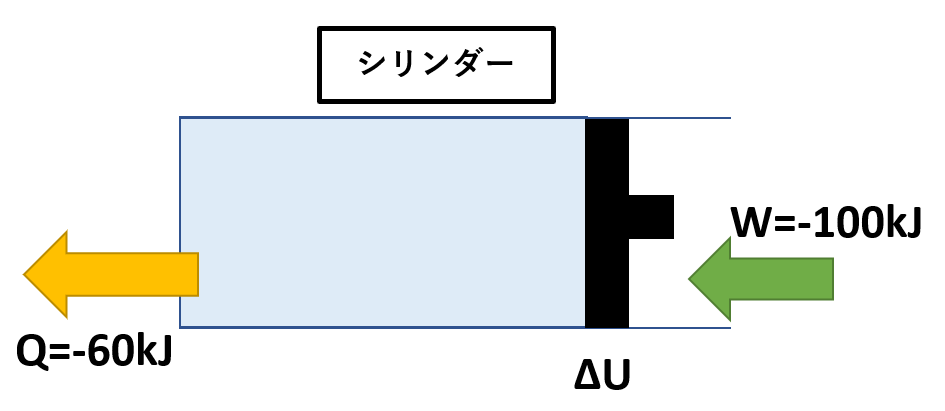
(2)ピストンによって気体の圧縮を行い、気体に対してW=100kJの仕事を与えた。このとき、シリンダーを通して外部へ熱量Q=60kJの熱が逃げたとすると、気体の内部エネルギーの変化量ΔUはいくらになるか。また、気体の温度は上昇したか、減少したか。
【解答】
(1)エネルギー式より、
Q=ΔU+W
W=Q-ΔU
=100-40
=60kJ
(2)エネルギー式より、
Q=ΔU+W
ΔU=Q-W
=-60-(-100)
=40kJ
内部エネルギーが上昇するので、温度は上昇する。
解答:(1)60kJ、(2)40kJ、温度は上昇
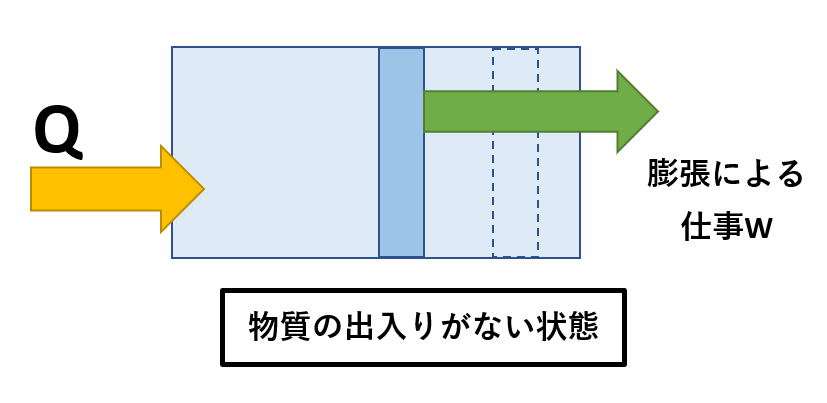
流動系のエネルギー式(エンタルピー)をわかりやすく解説
開いた系のエネルギー式で、取りだされる仕事を「工業仕事」と呼びます。
そして、式に関係するエネルギーはこんな感じです。
| 系に流入するエネルギー | 流体の内部エネルギーU₁
流体が系内に押し込まれる仕事p₁V₁ 系外から加えられる熱量Q 運動エネルギー1/2mc₁² 位置エネルギーmgz₁ |
| 系から流出するエネルギー | 流体の内部エネルギーU₂
流体が系内に押し込まれる仕事p₂V₂ 系外に取り出される仕事Wt 運動エネルギー1/2mc₂² 位置エネルギーmgz₂ |
これら上記のエネルギーの保存から、
U₁+p₁V₁+Q+1/2mc₁²+mgz₁=U₂+p₂V₂+1/2mc₂²+mgz₂+Wt
U+pV=Hとおいて、エンタルピーと呼ぶと、
H₁+Q+1/2mc₁²+mgz₁=H₂+1/2mc₂²+mgz₂+Wt
そして一般に、位置エネルギーは他に比べて小さく無視できるので、
H₁+Q+1/2mc₁²=H₂+1/2mc₂²+Wt
つまり、
Q=(H₂-H₁)+1/2m(c₂²-c₁²)+Wt(流体1kgあたりはq=(h₂-h₁)+1/2m(c₂²-c₁²)+wt)
※hは流体1kgあたりのエンタルピーで比エンタルピーと呼ぶ
と表すことができます。

なお、系の出入口の速度差が小さい場合、右辺第2項(1/2m(c₂²-c₁²))は無視できるため、
Q=(H₂-H₁)+Wt、あるいはQ=ΔH+Wt
が成り立ちます。
例題(開いた系のエネルギー式)
ここで例題を解いてみましょう。
【例題】
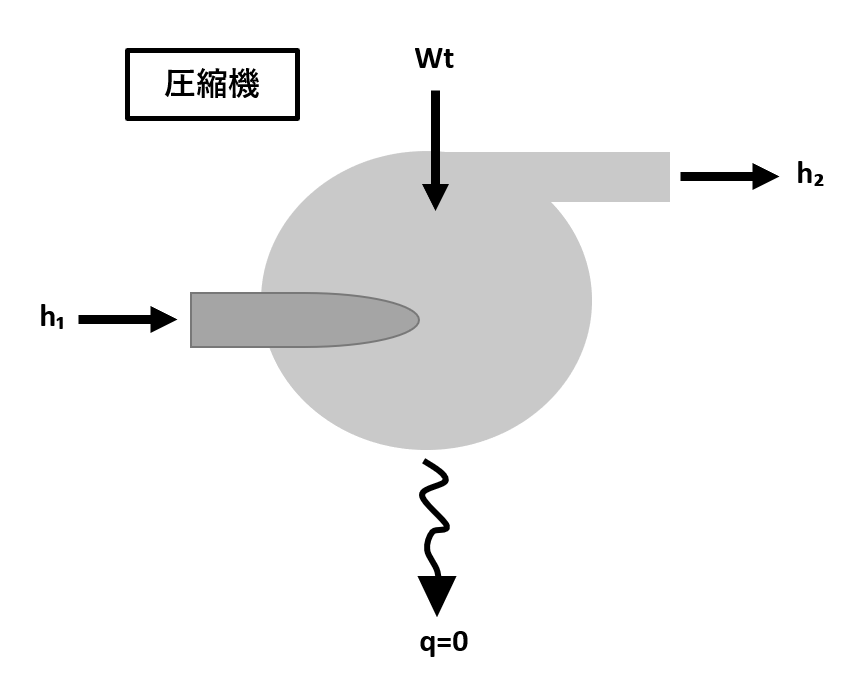
圧縮機を用いて、気体を圧縮することを考える。圧縮機入口での気体の比エンタルピーh₁=100kJ/kgであり、圧縮機出口の気体の比エンタルピーh₂=300kJ/kgであった。
周囲への熱損失は考えないものとして、圧縮機によって気体に対して行った仕事量wtはいくらか。
【解答】
流動系のエネルギー式において、エネルギー収支を考えるときに、機械のエネルギーが入ってくる流入分と機械からエネルギーが出ていく流出分に整理するとわかりやすくなります。
この場合、仕事量や熱量の出入りについて、符号は考えず、プラス(+)として扱いましょう。
よってエネルギー式は、
h₁+wt(流入分)=h₂+q(流出分)
wt=h₂-h₁+q
=300-100+0
=200kJ/kg
【解答】仕事量wt=200kJ/kg
また熱力学関連として、ボイルシャルルの法則については、また別記事でまとめていますので併せてご確認下さい。
エンタルピーをわかりやすく!意味や例題まとめ
ポイント
エンタルピーとは空気が持つ熱量(エネルギー)のことで、内部エネルギーと膨張・収縮するためのエネルギーを合わせたもの
流体1kgあたりのエンタルピーを比エンタルピーと呼ぶ
例題で計算の流れや公式をチェック!
以上です。
ありがとうございました。