今回のテーマは【浮力】
浮力とは、たとえば、ボールが水の中にあるとき、ボールは鉛直上向きの力を受けます。
この力が【浮力】です。
公式や求め方についてまとめました。
さらに計算問題も載せておきましたので、ぜひチャレンジしてみてください。
それではさっそく参りましょう、ラインナップは目次からどうぞ 🙂
目次
浮力の公式と求め方をわかりやすく解説！計算問題＆解説付き
まずは【浮力】の定義について確認していきましょう。
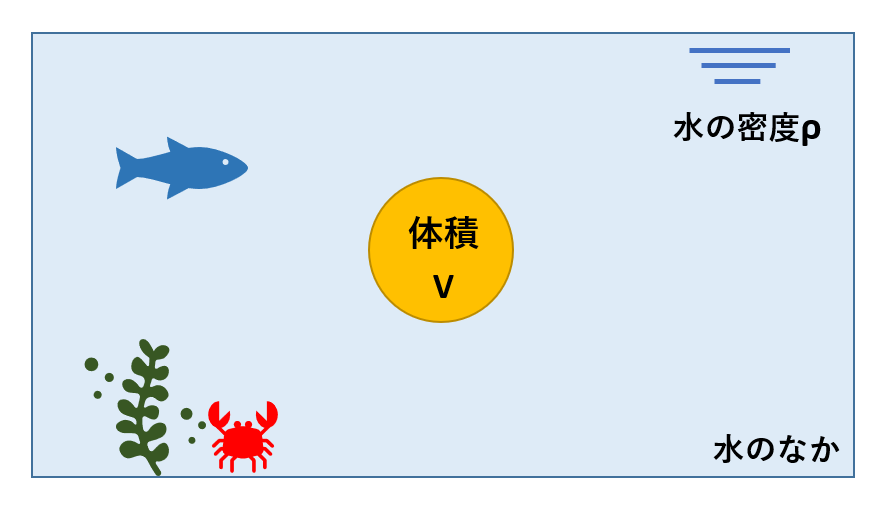
体積Vの物体が密度ρの静止した液体中にあるとき、物体は鉛直上向きの力、すなわち【浮力】Fを受けます。
重力加速度をgとすると、この浮力Fは、
浮力F=ρgV
と表すことができます。
また上記の公式から、浮力は物体が排除した体積の液体の重量と同じことがわかりますね。
すなわち、静止中の物体は、浮力分だけ軽くなっており、これを【アルキメデスの原理】と定義されていますので覚えておきましょう。
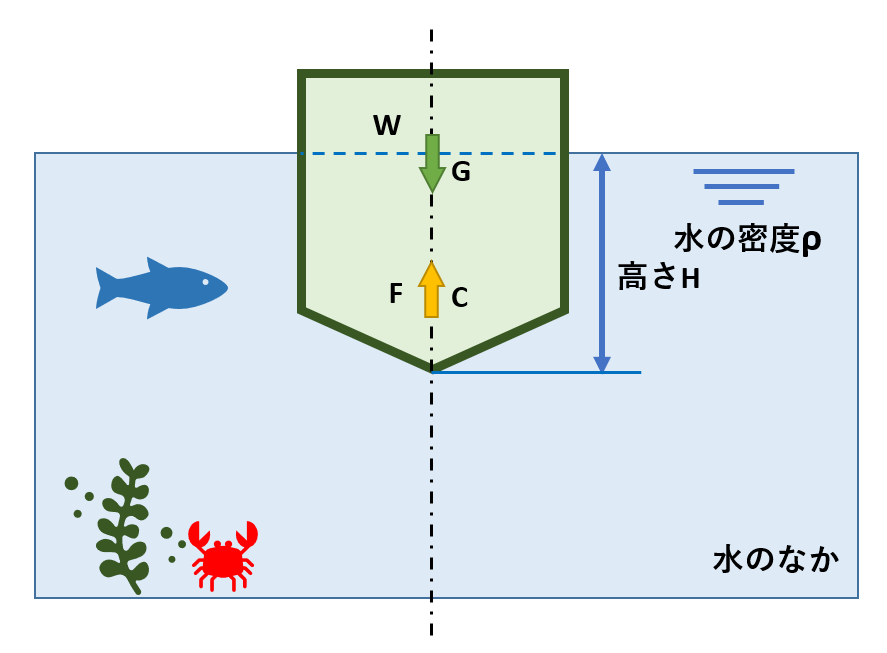
また、上記の図のように、浮力によって液体中に浮かんでいる物体を「浮揚体（ふようたい）」といいます。
このとき、物体の重さWと浮力Fは等しいです。
物体の体積Vのうち、液中にある体積をV’、すなわち浮揚体である物体が排除した液体の体積V’を「排水量」とも言います。
物体の重さWと浮力Fおよび、排水量V’の間には、以下の関係が成り立ちます。
W=F=ρgV’
そして重心Gと浮力Fの作用点Cを結ぶ鉛直線を浮揚軸、液面による浮揚体の切断面を浮揚面と定義されています。
一方、浮揚面から物体の最下部までの深さを【喫水（きっすい）】と呼びますので覚えておきましょう。
つづいては以下の図をご覧ください。
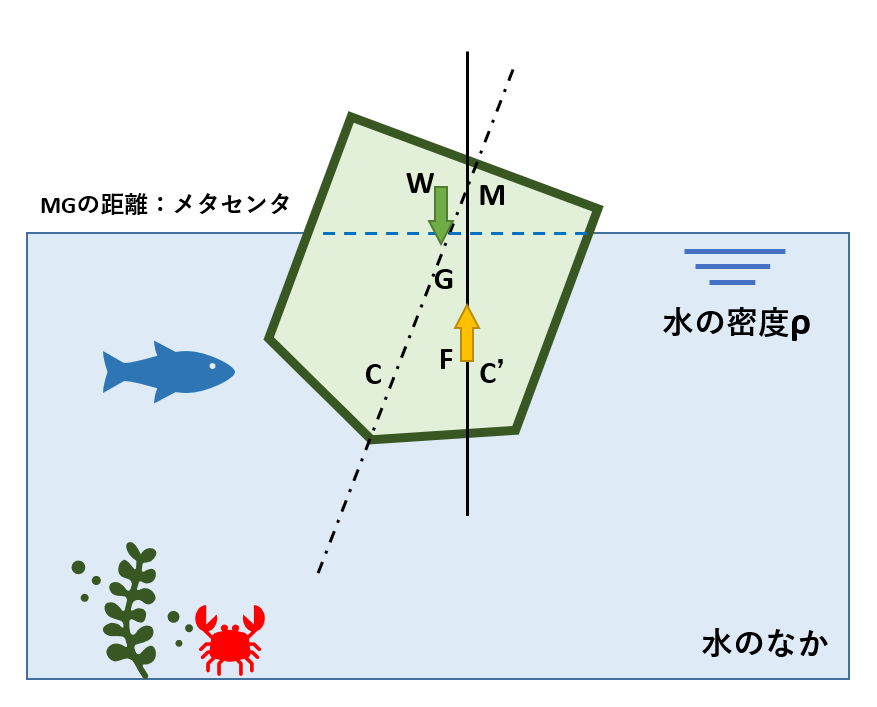
上記図のように、浮揚体がつり合いの状態から角度θだけ傾斜すると、浮揚の作用点はCからC’に移動し、これにより浮力Fと物体の重さWによるモーメントが働きます。
この場合、新しい浮力の作用線と浮揚軸が交わる点を【メタセンタ】、重心GとメタセンタMとのキョリを、「メタセンタの高さ」と呼んでいます。
メタセンタMが重心Gより高い位置にあるときは、元のつり合い状態に戻ろうとする復元偶力が生じ、浮揚体は安定している状態です。
| 状態（図解） | 公式 | 解説 |
|
浮力F=ρgV | 浮力：F
物体の体積：V 物体の密度：ρ 重力加速度：g |
|
W=F=ρgV’ | 物体の重さ：W
排水量（物体が水に入っている部分）：V’ 浮力：F 物体の密度：ρ 重力加速度：g |
浮力の計算問題（解答付き）
それではココで、計算問題を解いてみましょう。
ぜひチャレンジしてみてください。
【例題】
空気中での重さが500Nであった物体を水中で測定すると300Nであった。
物体の体積と比重を求めよ。なお、重力加速度g=9.81m/s²、水の密度ρ=1000kg/㎥とする。
【解答】
まず、空気中での重さが500Nであった物体を水中で測定すると300Nであった。という文章から、
浮力F=500-300=200Nであることが分かります。
よって浮力の公式を使って、
F=ρgV
体積V=F/ρg=200/(1000×9.81=0.0204㎥
比重は空気中と水中の比であるから、
比重s=(500/9.81)/(200/9.81)=2.50
解答：物体の体積V=0.0204㎥、比重s=2.50
浮力の公式と求め方をわかりやすく解説まとめ
| 状態（図解） | 公式 | 解説 |
|
浮力F=ρgV | 浮力：F
物体の体積：V 物体の密度：ρ 重力加速度：g |
|
W=F=ρgV’ | 物体の重さ：W
排水量（物体が水に入っている部分）：V’ 浮力：F 物体の密度：ρ 重力加速度：g |
以上です。
ありがとうございました。