ばね定数とは、ばねの伸び縮みに関連する比例定数で、一般的にkで表されます。
たとえば、ばねにF【N(ニュートン)】の力を加えたとき、x【m】伸びた(または縮んだ)とすると、
F=kx
※k[N/m]:ばね定数
が成り立ちます。
また実験によれば、加える力が小さいときは物体の変形の大きさは加えた力に比例し、この関係を【フックの法則】というので合わせて覚えておきましょう。
目次
ばね定数の求め方
ばね定数は、ばねのつなぎ方によって求め方が変わります。
ばね定数の求め方
- 直列につないだ場合
- 並列につないだ場合
1.直列につないだ場合
.png)
ばね定数k₁、k₂の2本のばねを直列につなぎ、力Fを加えて引っ張ります。
それぞれの伸びがx₁、x₂であったとすると、この場合どちらのばねにも力Fが加わっているので、
F=k₁x₁=k₂x₂
が成り立ちます。
そして全体を1本のばねと考えたときのばね定数をKとすると、全体の伸びは(x₁+x₂)であるから、
F=K(x₁+x₂)=K(F/k₁+F/k₂)
よって、
1/K=1/k₁+1/k₂
という公式が成り立ちます。
2.並列につないだ場合
.png)
ばね定数k₁、k₂の2本のばねを並列につなぎ、力Fを加えて引っ張ったところ、どちらもxだけ伸びたとします。
それぞれのばねに加わる力をF₁、F₂とすると、
F₁=k₁x
F₂=k₂x
全体を1本のばねと考えたときのばね定数をK’とすると、全体に加える力は
F=F₁+F₂であるから、
F=F₁+F₂=k₁x+k₂x=(k₁+k₂)x
この式をFK’xと比較することにより、
K’=k₁+k₂
が成り立ちます。
| ばねのつなぎ方 | ばね定数の求め方 |
| ばねを直列につないだ場合 | 1/K=1/k₁+1/k₂ |
| ばねを並列につないだ場合 | K’=k₁+k₂ |

ばね定数の例題(組み合わせ)
ここでひとつ、ばね定数に関連した例題を解いてみましょう。
ぜひチャレンジしてみてください。
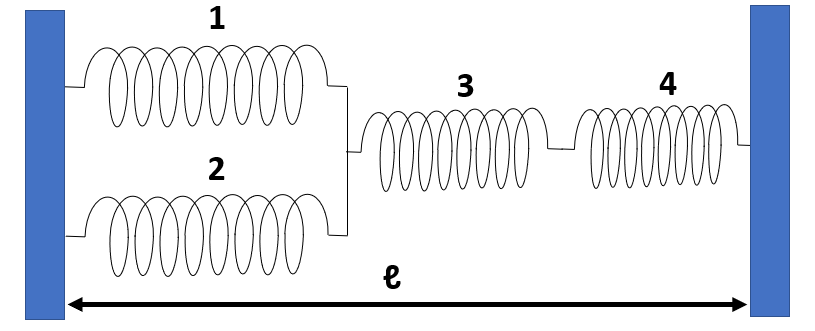
〈例題〉
ばね定数k、自然の長さℓ₀のばね4本をつないで、距離ℓだけ離れた壁の間に張りました。
ただし、ℓ>3ℓ₀とします。
(1)全体を1本のばねと考えたときのばね定数を求めなさい。
(2)ばね1の伸びはいくらか求めなさい。
(1)解答
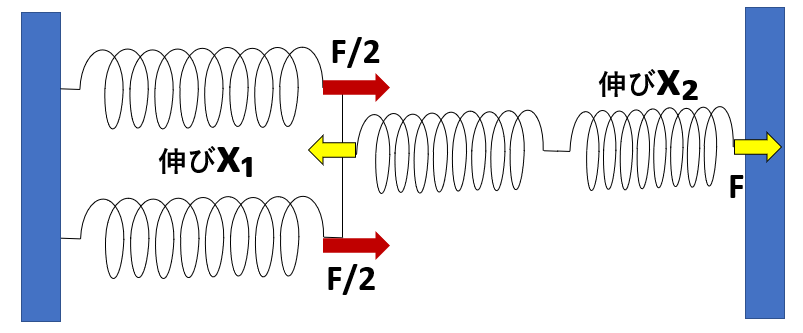
ばねを直列につなぐと、どのばねにも同じ大きさの力が加わり、ばね定数が等しいばねを並列につなぐと、両方のばねに同じ大きさの力が加わります。
ℓ>3ℓ₀だから、ばねはすべて伸びています。
ばね3、ばね4に加わっている力をFとすると、ばね1、ばね2に加わっている力はF/2です。
ばね1、ばね2の伸びをx₁、ばね3、ばね4の伸びをx₂とすると、
フックの法則により
F/2=kx₁…①
F=kx₂…②
全体の伸びは(ℓ-3ℓ₀)であるから、
ℓ-3ℓ₀=x₁+2x₂…③
③式に①、②式からx₁、x₂を代入すると、
ℓ-3ℓ₀=F/2k+2F/k=5F/2k
よってF=2k/5(ℓ-3ℓ₀)…④
全体を1本のばねと考えたときのばね定数をKとすると、
F=K(ℓ-3ℓ₀)…⑤
④と⑤の式を比較して、K=2k/5
解答 K=2k/5
(2)解答
①式と④式より、
x₁=F/2k=(ℓ-3ℓ₀)/5
解答 x₁=(ℓ-3ℓ₀)/5
以上です。
ありがとうございました。
