
例えばボールをなげたり、スマホを落としたり。

ってなわけで、今回のテーマは【放物運動】
公式や計算例題をわかりやすく解説していきます。

目次
放物運動をわかりやすく解説!公式の覚え方&計算例題付き
放物運動は、水平に投げた物体と、斜めに投げ上げた物体の運動の2つに分類できます。
それぞれ見ていきましょう。
放物運動をわかりやすく➀水平に投げた物体の運動
以下の図解をみてください。
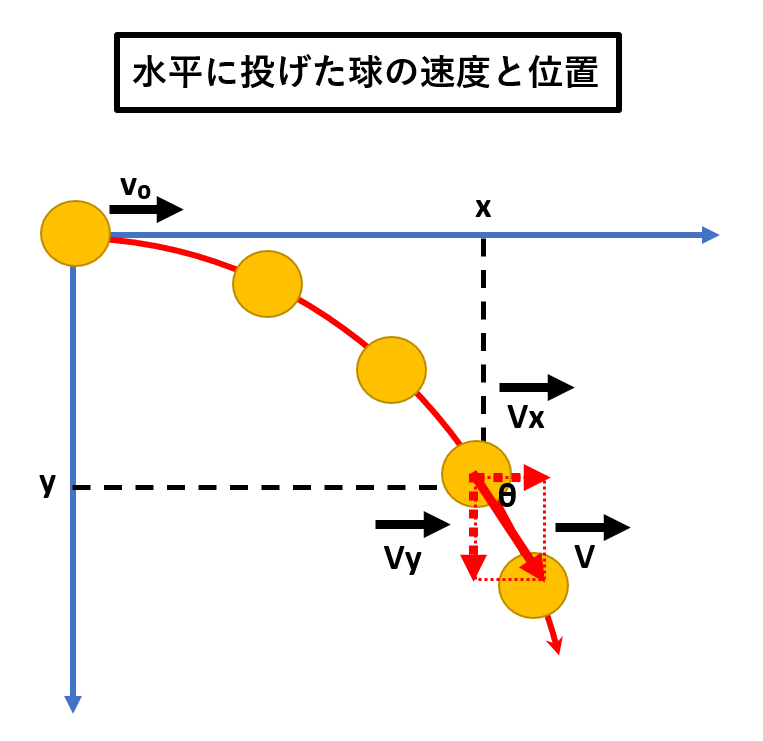
水平方向に投げたボールは、放物線を描いて地面に落ちますよね。
このとき、ボールには重力だけが働いています。
重力は鉛直下向きで、水平方向の力は0であるから、物体には水平方向の加速度は生じていないことがわかります。
したがって、投げ出したときの初速度をV₀とすると、t秒後の速度の水平成分VxもV₀のまま、ということです。
V₀(投げ出したときの初速度)=Vx(t秒後の速度の水平成分)
一方で、鉛直方向には重力加速度gの等加速度運動をします。
初速は水平方向であり、鉛直成分は0であるから、t秒後の速度の鉛直成分Vyは以下のようになります。
t秒後の速度の鉛直成分Vy=gt
よってt秒後の速度の大きさは、
V=√(Vx²+Vy²)=√(V₀²+(gt)²)
となります。
そして速度ベクトルの向きは、Vが水平方向となす角をθとすると、
tanθ=Vy/Vx=gt/V₀
水平方向には等速運動をするので、t秒後の物体の位置のX座標はX=V₀t…①
鉛直方向には初速度0、加速度gの等加速度運動をするので、t秒後の物体の位置のy座標はY=(1/2)×gt²…②
①、②の式からtを消去すると、
Y=(g/2V₀²)X²
という式が得られます。
これが物体の軌道を表す式であり、数学的に言えばこの式は2次関数であるから、軌道は放物線になることが分かります。
| 放物運動(水平)公式 | |
| 速度
水平方向は初速度V₀の等速運動 鉛直方向は初速度0、加速度gの等加速度運動 |
V₀(投げ出したときの初速度)=Vx(t秒後の速度の水平成分)
t秒後の速度の鉛直成分Vy=gt |
| t秒後の物体の位置 | X=V₀t
Y=(1/2)×gt² |
水平の放物運動の計算例題

【例題】
高さ1000mの所を200m/sの速度で水平に飛んでいる飛行機から、A点の真上で物体を静かに投下した。物体が落下する時間、A点と落下点とのキョリ、および地面に落下する直前の物体の速さを求めなさい。
ただし、空気抵抗は無視するものとし、重力加速度gは9.8m/s²する。
【解答】
着眼点としては、飛行機のなかにある物体は、飛行機と同じ速度で飛んでいるため、飛行機から物体を落とすのを地上から見ると、この物体は水平に投げ出されたのと同じ運動をするということです。
物体の初速度は水平方向に200m/sで、鉛直成分は0であるから、鉛直方向の運動は自由落下運動と同じです。
よって落下する時間をtとして公式に当てはめると、
1000=(1/2)gt²
t=√(2×1000/g)=√(2000/9.8)≒14.3s
またA点と落下点とのキョリXmは、水平方向の変位を求めればよいため、
X=V₀t=200×14.3=2860m
最後に落下直前の速さは、水平成分Vxと鉛直成分Vyを求めます。
Vx=V₀=200m/s
Vy=gt=9.8×14.3=140m/s
したがって速さVは三平方の定理より
V=√(Vx²+Vy²)=√(V₀²+(gt)²)=√(200²+140²)≒244m/s
となります。
解答:t=≒14.3s、X=2860m、V≒244m/s
また物理関連としては、仕事についてまた別記事でまとめていますので、併せてチェックしてみてください。
放物運動をわかりやすく②斜めに投げ上げた物体の運動
つづいては、斜めに投げ上げた物体の運動についてです。
斜めに投げ上げる場合も、水平と同じで水平方向には等速運動を行います。
ただし、力を分解して考えるため、式は以下のようになります。
Vx=V₀cosθ
鉛直方向では、初速度、加速度-gの負の等加速度運動をするため、t秒後のY方向の速度は
Vy=V₀sinθ-gt
そして物体がt秒後に位置する座標は、
X=V₀tcos達するじ
Y=V₀sinθ-(1/2)gt²…②
①②からtを消去してxとyの関係式を求めると、
y=xtanθ-gx²/(2V₀²cos²θ)となり、この式が物体がたどる軌道を表す式となります。
| 放物運動(斜めに投げ上げた物体)公式 | |
| 速度 | Vx=V₀cosθ
Vy=V₀sinθ-gt |
| t秒後の物体の位置 | X=V₀tcosθ
Y=V₀sinθ-(1/2)gt² |
ちなみに物体が最高点に達した時、速度の鉛直成分は0となるので、
0=V₀sinθ-(1/2)gt²より、
t=V₀sinθ/g
Y=V₀sinθ-(1/2)gt²の式に代入すると、最高点の高さYを求めることができます。
Y=V₀sinθ-(1/2)g×(V₀sinθ/g)²
=V₀²sin²θ/2g
一方、投げ上げた物体が投げた地点と同じ高さまで落ちると、Y座標は0になります。
そこでY=V₀sinθ-(1/2)gt²の式においてY=0とすると、物体が落下する時刻tが求められます。
0=V₀sinθ-(1/2)gt²
t=2V₀sinθ/g

このtをX=V₀tcosθの式に代入すると、
X=V₀×(2V₀sinθ/g)×cosθ
=2V₀sinθcosθ/g
=V₀²sin2θ/g(※2sinθcosθ=sin2θ)
となります。
斜めの放物運動の計算例題
ここでまたまた、例題を解いてみましょう!
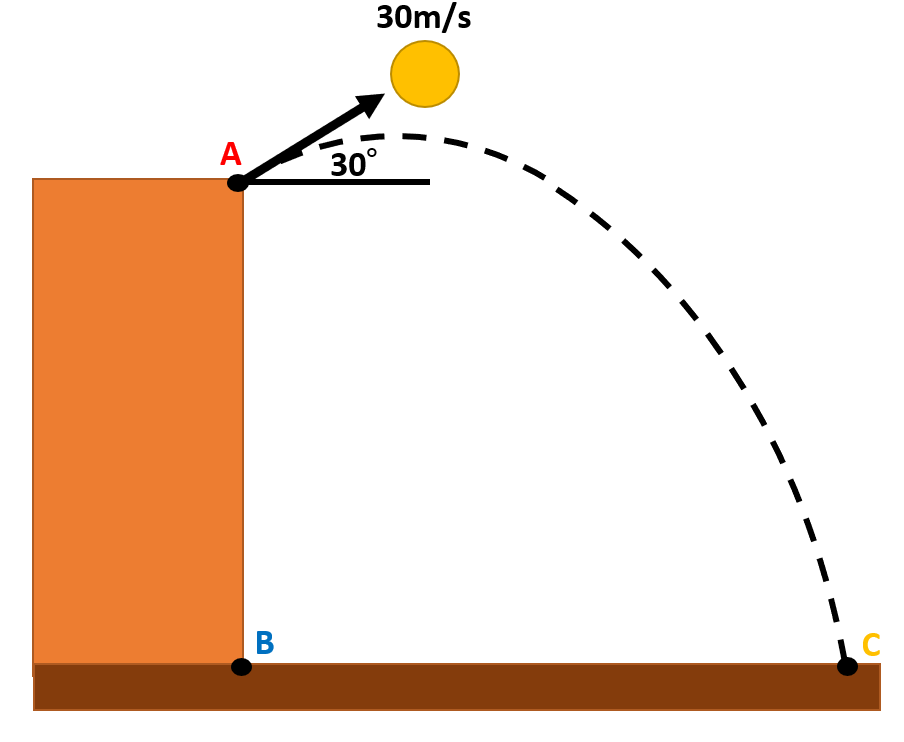
【例題】
高さ50mの崖のうえのA点から石を30m/sの速さで水平方向と30°の角をなすように投げると、石は地上のC点に落下した。重力加速度を10m/s²として、次の問いに答えなさい。
(1)石がC点に達するまでの時間はいくらか。
(2)AC間の距離はいくらか。
【解答】
ポイントとしては、石を投げだした点を原点にとり、鉛直上向きをy軸の正の向きにとれば、C点の座標は-50mとなることです。
(1)A点を原点とし、水平方向にX軸、鉛直方向にY軸をとります。
そうすると初速度の水平成分Vx、Vyは、
Vx=V₀xcosθ=30×cos30°=15√3m/s
Vy=V₀ysinθ=30×sin30°=15m/s
C点のy座標はy=-50mであるから、
Y=V₀sinθ-(1/2)gt²
-50=15t-(1/2)gt²=15t-5t²
よってt=5、-2
t>0であるから、t=5s
(2)Aの真下でCと同じ高さの点をBとすると、BCの長さはC点の座標のx座標で与えられます。
BC=V₀xt=15√3×5≒15×1.73×5.0≒130m
よってAC=√(AB²+BC²)=√(50²+130²)≒139m
解答:(1)t=5s (2)139m
放物運動をわかりやすく解説!公式の覚え方まとめ
公式の覚え方:放物運動は水平と斜めで分けて考えるとよい
| 放物運動(水平)公式 | |
| 速度
水平方向は初速度V₀の等速運動 鉛直方向は初速度0、加速度gの等加速度運動 |
V₀(投げ出したときの初速度)=Vx(t秒後の速度の水平成分)
t秒後の速度の鉛直成分Vy=gt |
| t秒後の物体の位置 | X=V₀t
Y=(1/2)×gt² |
| 放物運動(斜めに投げ上げた物体)公式 | |
| 速度 | Vx=V₀cosθ
Vy=V₀sinθ-gt |
| t秒後の物体の位置 | X=V₀tcosθ
Y=V₀sinθ-(1/2)gt² |
以上です。
ありがとうございました。
.png)