電気回路をわかりやすく！公式一覧（交流回路・直流回路・並列回路）仕組みまとめ

電気回路をわかりやすく教えて！

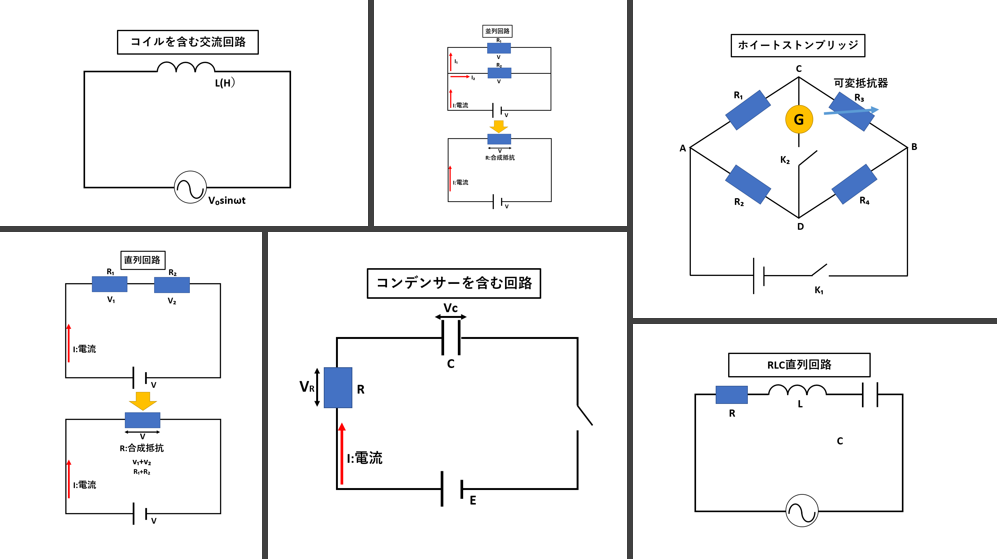
電気回路って色んなパターンがあって難しいですよね。

そんなわけで今回は、基本的な電気回路を図解を使って分かりやすく解説しました。

また交流回路や直列回路などの公式を一覧にまとめましたのでサクッと確認したい時にもぜひご覧ください。

それではさっそく参りましょう、ラインナップは目次からどうぞ 🙂

電気回路をわかりやすく！公式＆仕組みをしっかり理解しよう

まずは電気回路の基本的な知識と公式から！

電気回路の定義とは？

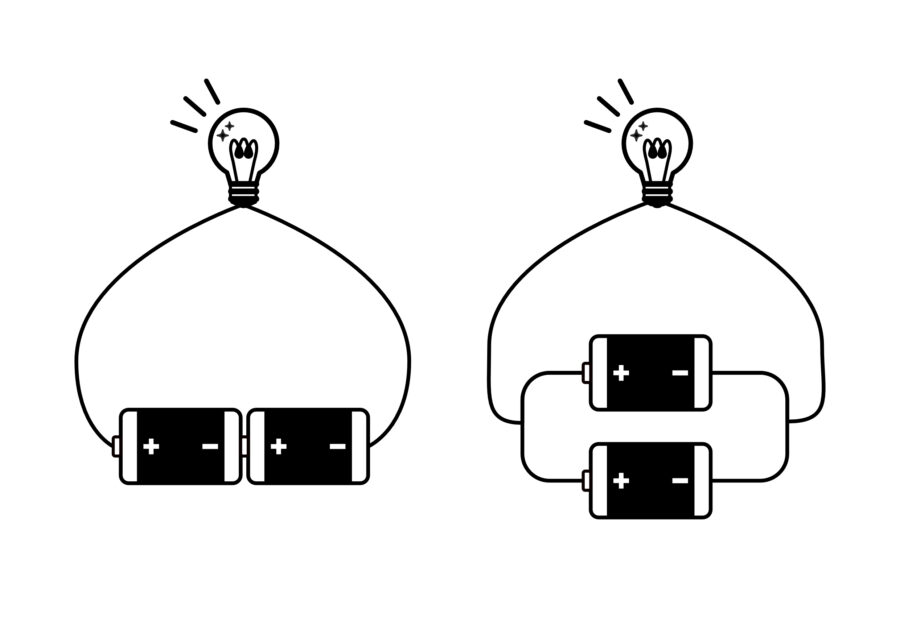
たとえば上記のイラストのように、豆電球を金属導線で接続すると、豆電球は点灯します。

この現象は、導線や電球のフィラメントに電流が流れたためです。

このような電気の流れを電流と言い、電流の流れる道筋は、図のように1周まわって戻る輪になっています。

これを電気回路、または単に回路と呼んでいます。

つまり、電流の流れがひとつの輪となって、スタート地点に戻ってくるものが【電気回路】なのです。

電流の向きについて

電流の向きは、正の電荷が移動する向きと定義されます。

電池に導線をつなぐとき、電流は正極から負極へ向かって流れます。

導体中の電流の正体は、負の電荷をもつ自由電子の流れであり、クーロン力によって負極から正極へ移動しているのです。

よって電流の向きは、電子の流れる向きと逆向きであることがポイントです。

電流の大きさと単位

電流の大きさは、導体の断面を1秒間に通過する電気量で表されます。

1秒間に1クーロン（記号C）の電荷が通過するような電流の大きさを1アンペアと定義しています。

したがって、導体の断面をt(s)の時間のあいだにQ(c)の電荷が通過するときの電流の大きさIは以下の式となります。

式：I（電流）＝Q（通過する電荷の量）/t（時間）

ちなみに1A（アンペア）＝1（C/s）

1Aの1/1,000を1ミリアンペア（mA）と呼びます。

電気回路をわかりやすく！基本的な電気回路の種類と公式一覧

直列回路の仕組み＆公式

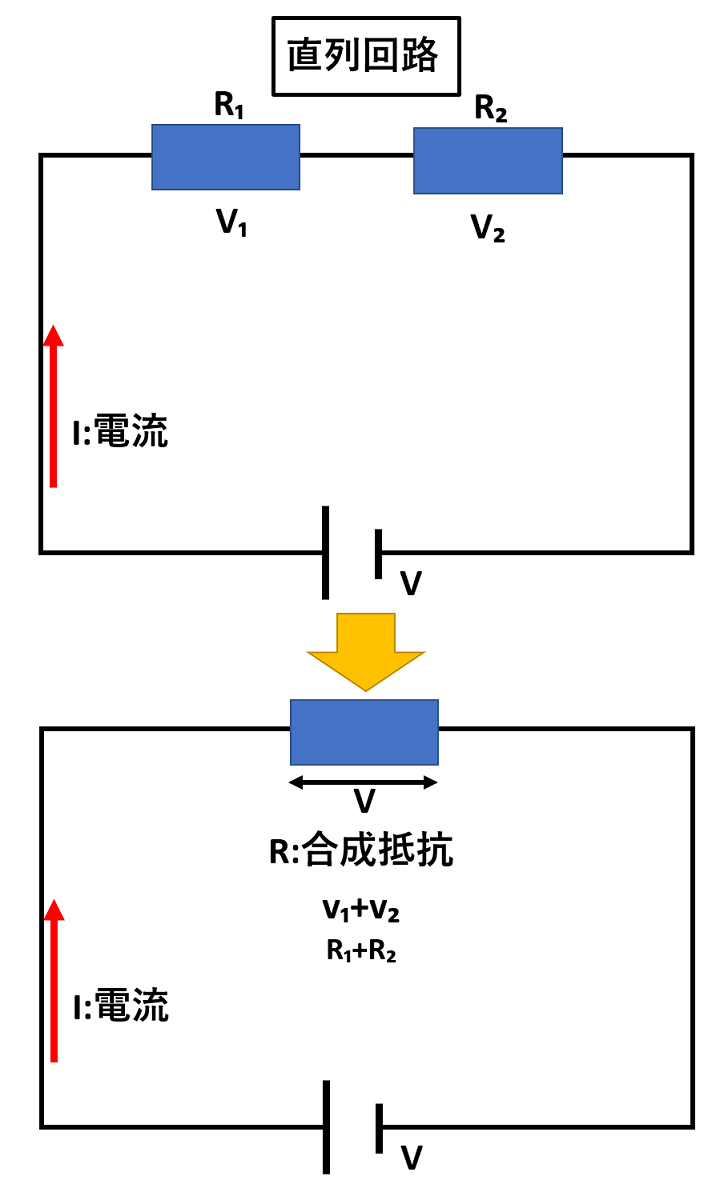
上記の図解のように、電流の流れる道筋が1本となるようにつなぐことを直列接続と言い、直列回路とも呼びます。

直列につないだ抵抗に電圧を加えると、電流が流れ、それぞれの関係は以下のとおりです。

V₁＝R₁I

V₂＝R₂I

また抵抗の直列接続では、各抵抗による電圧降下の和は、電源端子間の電圧と同じです。

つまり、

V=V₁+V₂

となります。

さらにR₁とR₂を直列につないだものと同じ働きをもつ抵抗を合成抵抗といいます。

公式としてはこんな感じです。

V＝RI（オームの法則）

R＝R₁+R₂+…（直列接続の合成抵抗）

このように直列接続の合成抵抗は、各抵抗値の和に等しいです。

この関係は抵抗が3個以上になっても成り立ちます。

並列回路の仕組み＆公式

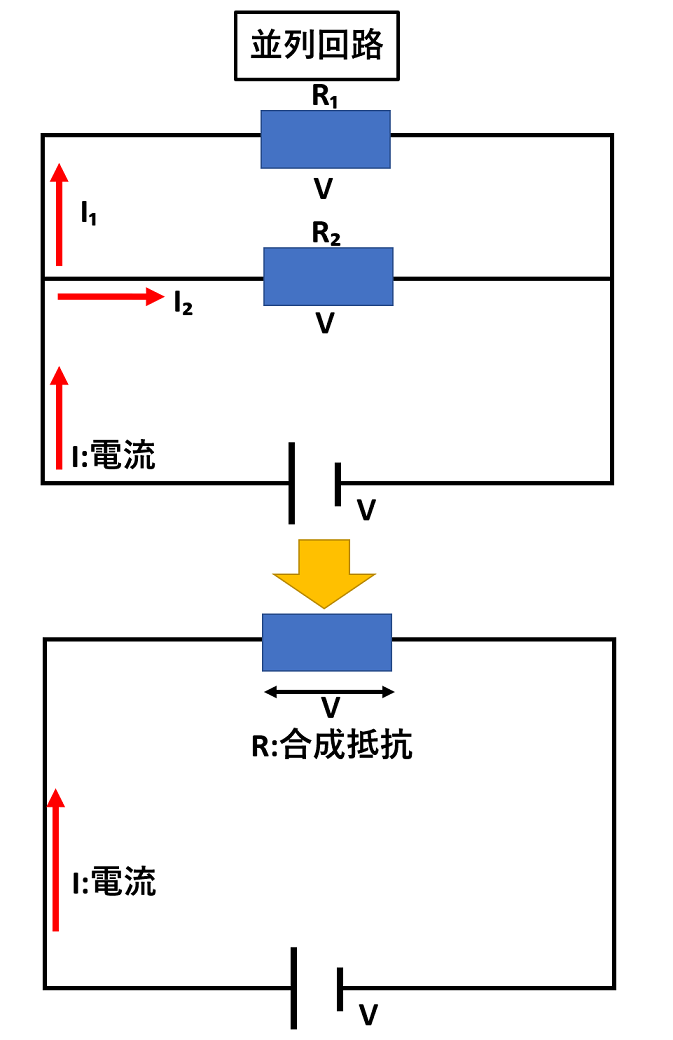
上記のイラストのように、電気抵抗をつなぎ、電源から出た電流が枝分かれして流れるようにする方法が並列接続であり、並列回路のことです。

並列回路のポイントは、R₁にもR₂にも同じ電圧Vがかかっていることです。

基本的な公式はこちら 🙂

I＝I₁+I₂

I₁＝V/R₁

I₂＝V/R₂

また直列回路と同じように、抵抗R₁とR₂を並列に接続したものとまったく同じ働きをする1つの抵抗を合成抵抗といいます。

公式はこちら 🙂

V＝RI（オームの法則）

V/R＝V/R₁+V/R₂+…すなわち1/R＝1/R₁+1/R₂（並列接続の合成抵抗）

ホイートストンブリッジの仕組み＆公式

ホイートストンブリッジは以下の図解のような回路で構成されています。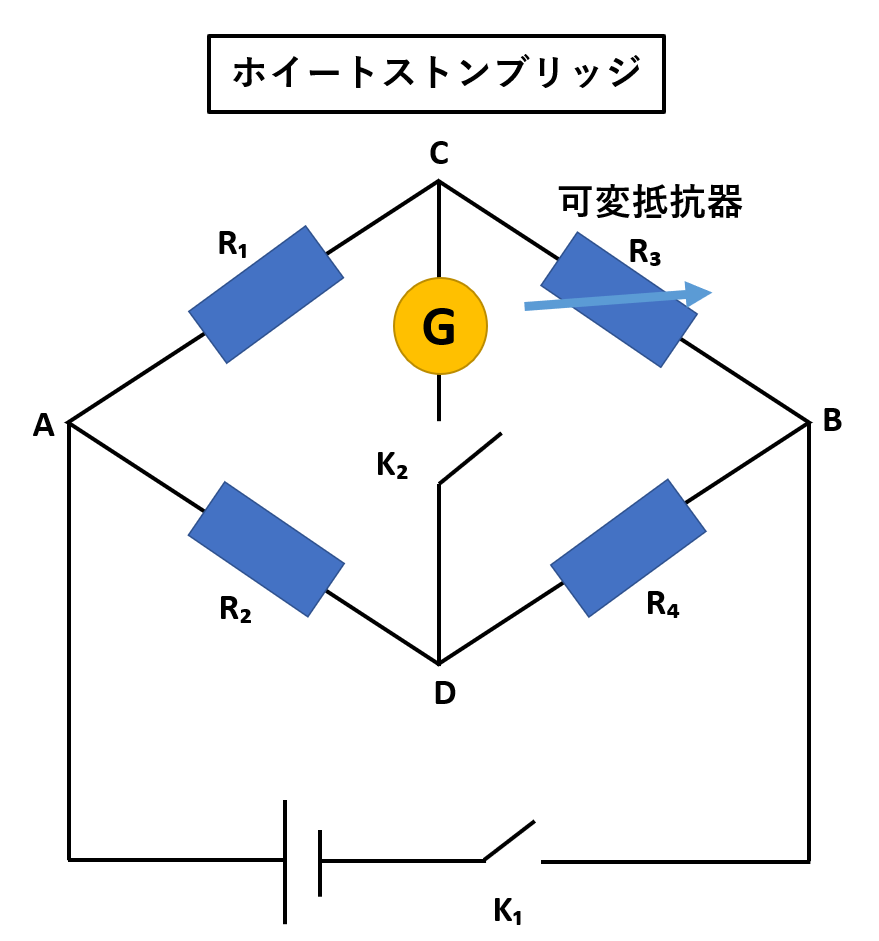

R₁、R₂は抵抗値が既知の精密抵抗器、R₃は抵抗値を変えられる可変抵抗器、R₄が抵抗値を測定しようとする抵抗器のこと。

Gは微弱な電流を測定する検流計です。

スイッチK₁を閉じて回路に電流を流すと、CD間にふつう電位差が生じますが、R₃の抵抗値を調節するとCD間の電位差は0となり、スイッチK₂を閉じても検流計Gに電流が流れないようにすることができます。

この時に成り立つ式は以下のとおりです。

R₁I₁＝R₂I₂

R₃I₁＝R₄I₂

よって、

R₁/R₃＝R₂/R₄、R₄＝R₂×R₃/R₁

となり、R₄の値を求めることができます。

コンデンサーを含む直列回路の仕組み＆公式

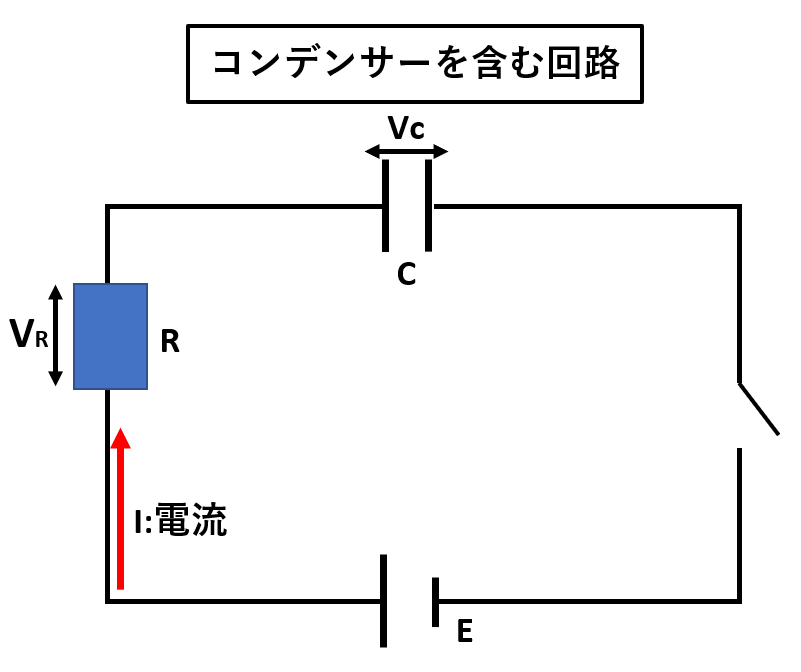
コンデンサーは極板間が絶縁されているので、基本的に電流は流れません。

しかしコンデンサーを充電したり放電したりする過程では、あたかもコンデンサーを通って電流が流れるような現象が起こります。

上記の回路のスイッチをいれると、電池の－極からコンデンサーの負極板に電子が移動し、コンデンサーの正極板から電池の＋極へ移動します。

この現象は、電池のプラス極とマイナス極が導体でつながっていることと同じです。

また、コンデンサーに電荷が蓄えられると、極板間に電圧Vcが生じます。

Vcの大きさは、はじめ電荷がないときは0ですが、電流が流れ始めると以下のグラフのように変化します。

【コンデンサーの電圧と電流】

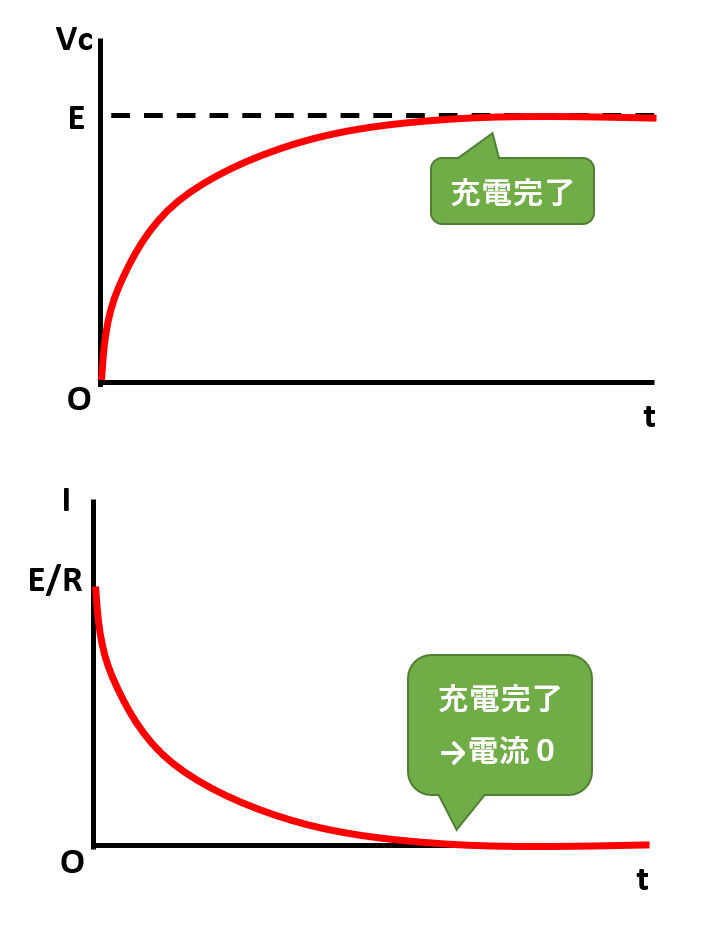
Vc＝Eになると充電は完了し、Vcはそれ以上増えません。

このように、コンデンサーの充電にはある程度の時間がかかり、抵抗や電気容量が大きいほど長い時間がかかります。

回路に流れる電流と抵抗値R,電圧降下Vの関係は、

E＝VR+Vcより、VR＝E-Vcとなるから、

I=VR/R＝（E-Vc）/R

となります。

交流回路（コイル、コンデンサー、RLC）の仕組み＆公式一覧

たとえば、磁界中でコイルを一定の速さで回転させると、コイルを貫く磁束が周期的に変化するので、コイルの両端に周期的に変化する誘導起電力が発生します。

このような電圧を交流電圧、それによって流れる電流を交流電流と呼びます。

交流におけるさまざまな回路を見ていきましょう。

コイルを含む交流回路

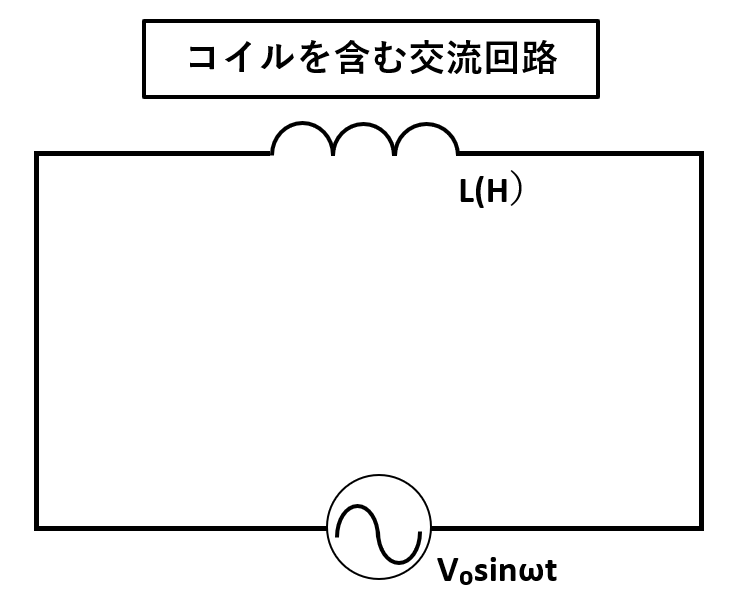
上記の図解のような、電気抵抗が無視できる理想的なコイルの場合、電圧と電流の式は以下のとおりです。

また、コイルを流れる交流の位相をグラフ化するとこんな感じです。（以下、図解参照）

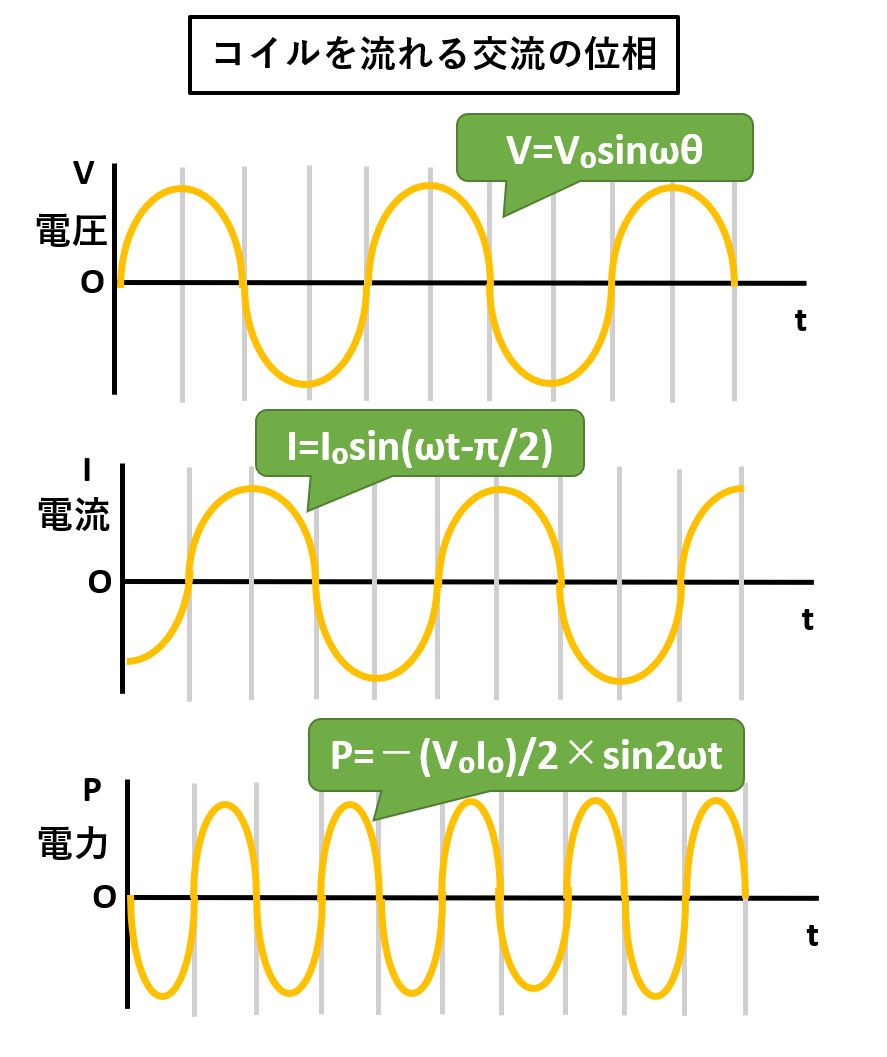
電流と電圧の位相がずれるため、電力Pのグラフは上記のようになります。

このように、電力に正負ができるため、電力Pの平均値は0（ゼロ）です。

コンデンサーを含む交流回路

コンデンサーに直流電圧をかけると、充電が完了するまでは導線に電流が流れますが、充電が完了すると電流は流れなくなります。

しかし交流電圧を加えると、コンデンサーは充電と放電をくりかえすので、導線には電流が流れ続けます。

また、電圧と電流の位相の関係は以下のとおりです。

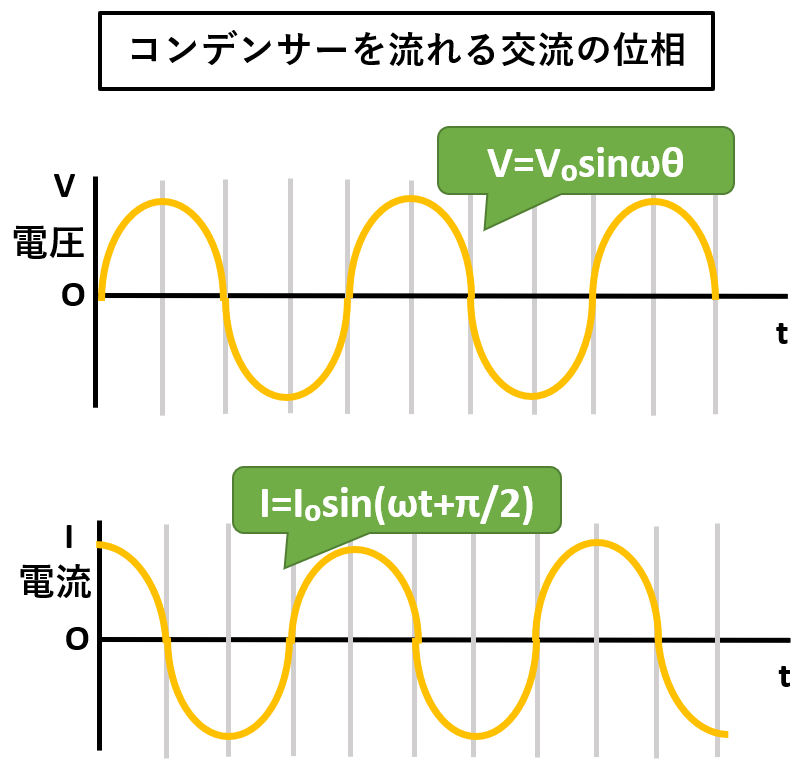
グラフから分かるとおり、コンデンサーを流れる交流電流の位相は、電圧の位相よりπ/2だけ進みます。

RLC直列回路

以下の図解のように、電気抵抗R、自己インダクタンスLのコイル、電気容量Cのコンデンサーを直列につないだものを、RLC直列回路といいます。

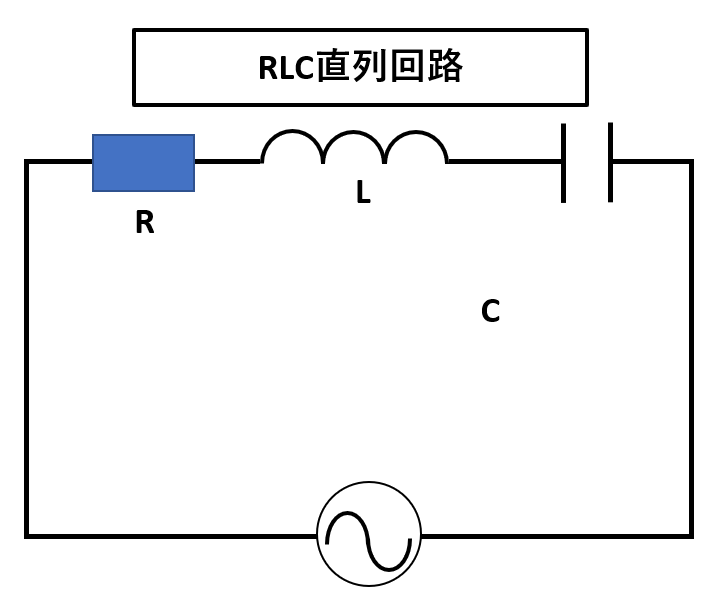
また、各部の電圧降下は以下のグラフに示したような時間変化が起こります。

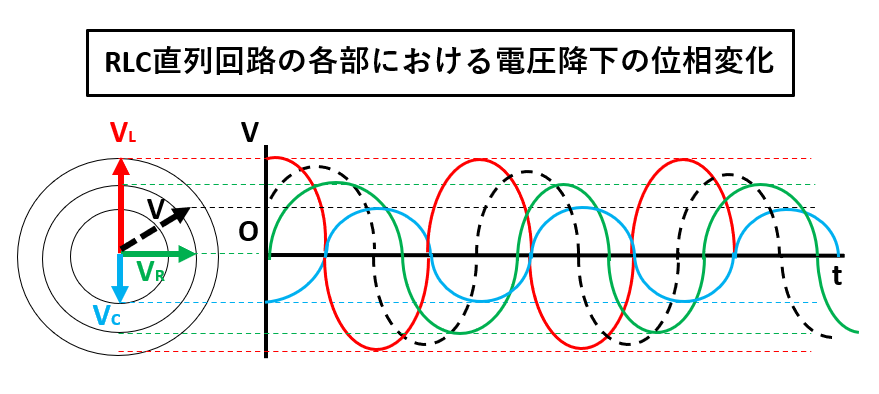
ごちゃごちゃしてますが（笑）、ポイントは、VL＞V＞VR＞Vcの順に波の幅は大きいことです。

さらにVLとVcはO点で重なります。

そして公式は以下のとおりです。

電流の位相は電圧の位相よりη（イータ）だけ遅れるため、

I＝I₀sin(ωt-η）

となります。

一方で、電気回路の図面記号などはまた別記事でまとめていますので併せてご確認ください。

電気回路をわかりやすく！公式一覧＆仕組みまとめ

電流の流れがひとつの輪となって、スタート地点に戻ってくるものが【電気回路】

回路を流れる電流の向きは、電子の流れる向きと逆向き

式：I（電流）＝Q（通過する電荷の量）/t（時間）

電気回路の種類	公式一覧	電気回路の図解
直列回路	V₁＝R₁I V₂＝R₂I V=V₁+V₂ V＝RI（オームの法則） R＝R₁+R₂+…（直列接続の合成抵抗）
並列回路	I＝I₁+I₂ I₁＝V/R₁ I₂＝V/R₂ V＝RI（オームの法則） V/R＝V/R₁+V/R₂+…すなわち1/R＝1/R₁+1/R₂（並列接続の合成抵抗）
ホイートストンブリッジ	R₁I₁＝R₂I₂ R₃I₁＝R₄I₂ R₁/R₃＝R₂/R₄、R₄＝R₂×R₃/R₁
コンデンサーを含む回路	E＝VR+Vcより、VR＝E-Vcとなるから、 I=VR/R＝（E-Vc）/R
交流回路（コイル）	電圧：V＝V₀sinωt 電流：I＝V₀/ωL×sin(ωt-π/2）※位相がπ/2ずれる
交流回路（コンデンサー）	電圧：V＝V₀sinωt 電流：I＝V₀/ωL×sin(ωt+π/2）※位相がπ/2進む
交流回路（RLC）	交流電圧V＝V₀sinωtをかけたとき 電圧：V＝I₀√R²+（ωL-1/ωC）² インピーダンス：Z＝√R²+（ωL-1/ωC）² 電圧の合成ベクトルと電流との位相差：η（イータ）＝（ωL-1/ωC）/R 電流：I＝I₀sin(ωt-η）

以上です。

ありがとうございました。