
今回のテーマは【レイノルズ数】について 🙂
レイノルズの公式のほか、層流や乱流の条件について確認していきましょう。
目次
レイノルズ数の乱流&層流の条件とは?公式も一覧でわかりやすく!
まずは定義から!
レイノルズ数の定義とは?
レイノルズ数とは、層流や乱流という水の流れのちがいを明確にしたもの。

実験の結果、流れる水の密度ρ、流速V、管の直径Dが大きいほど、また水の粘性係数μが小さいほど乱流が発生することを発見しました。
レイノルズ数の公式
レイノルズ数の公式は以下のとおり。
公式:Re=ρVD/μ
- Re:レイノルズ数
- ρ:密度
- V:流速
- D:管の直径
- μ:粘着係数
レイノルズ数の層流・遷移・乱流の違い
レイノルズ数は無次元数ですが、流れは2,300以下で層流、4,000を超えると乱流となり、2,300~4,000の間は中間領域で遷移状態にあります。
遷移状態とは層流から乱流(またはその逆)に変化する過程であり、不安定な状態と覚えておけばOKです。
| 層流
Re≦2,300 |
遷移
2,300<Re≦4,000 |
乱流
4,000<Re |
| 乱れのない水の流れ(インクの筋が乱れない) | 変化する過程であり、不安定な状態 | 乱れのある水の流れ
(速度を上げていくとインクの筋が広がりをみせ、混じり合いながら管の断面全体に拡散していく) |
また、層流から乱流に変化する時のレイノルズ数は【臨界レイノルズ数Rec】と呼ばれ、2300程度だとされています。
層流と乱流について!レイノルズ数の図解付き
層流と乱流について、さらにしっかりチェックしておきましょう。
たとえば、直径が一定でまっすぐで透明なアクリル樹脂の管のなかを流れる水をイメージしてみてください。
この管に水をゆっくりした速度で流し始め、次第に流速を上げてみます。
目で見やすいように管の中心の位置にインクを連続して注入してみると、以下の図解のようになります。
【レイノルズ数の図解】
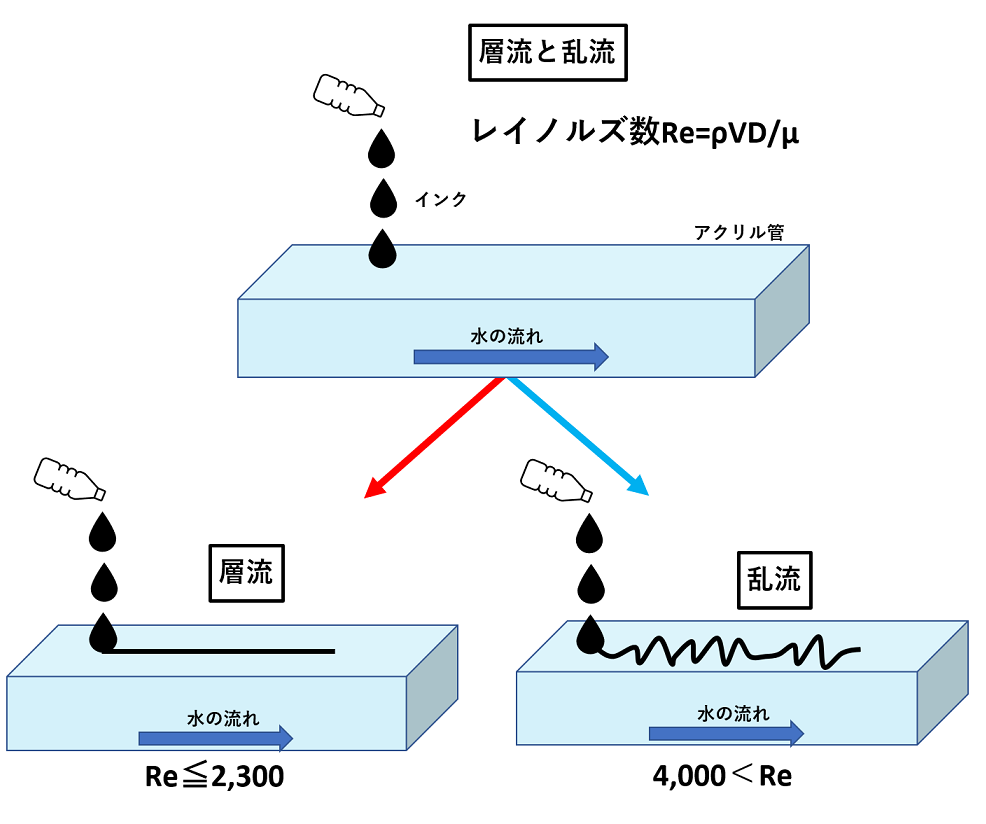
このとき、流れの遅い場所ではインクで着色されたみずは細く筋をひいてスーッと滑らかに伸びて流れていきます。
一方で、次第に速度を上げていくとインクの筋に乱れが生じはじめます。
さらに速度を上げるとインクは注入された直後から筋とはならずに広がり始め、さらに乱れることによって断面全体に拡散していきます。
このインクの筋がスーッと伸びる乱れのない水の流れを層流と呼びます。
これに対して、速度を上げていくとインクの筋が広がりをみせ、混じり合いながら管の断面全体に拡散していく乱れのある流れを乱流と呼びます。
| 層流 | 乱れのない水の流れ(インクの筋が乱れない) |
| 乱流 | 乱れのある水の流れ(速度を上げていくとインクの筋が広がりをみせ、混じり合いながら管の断面全体に拡散していく) |
一方、関連として波長グラフ、干渉などについては、それぞれ別記事でまとめています。
そのほか、物理・材料カテゴリーもぜひチェックしてみてください。
レイノルズ数の乱流&層流の条件とは?公式まとめ
レイノルズの公式:Re=ρVD/μ
- Re:レイノルズ数
- ρ:密度
- V:流速
- D:管の直径
- μ:粘着係数
層流から乱流に変化する時のレイノルズ数は【臨界レイノルズ数Rec】と呼ばれ、2300程度である
層流&遷移&乱流
| 層流
Re≦2,300 |
乱れのない水の流れ(インクの筋が乱れない) |
| 遷移
2,300<Re≦4,000 |
変化する過程であり、不安定な状態 |
| 乱流
4,000<Re |
乱れのある水の流れ
(速度を上げていくとインクの筋が広がりをみせ、混じり合いながら管の断面全体に拡散していく) |
以上です。
ありがとうございました。
.png)