今回のテーマは物理における波のグラフです。
いろいろな波のグラフについて図解でまとめましたのでぜひご覧ください。
また縦波と横波の違いもわかりやすく解説しています。
それではさっそく参りましょう、ラインナップは目次からどうぞ 😀
目次
物理の波長グラフ➀縦波と横波の違い
物理の波には縦波と横波、さらに粗密波(そみつは)と呼ばれるものもあります。
波の種類
- 横波
- 縦波
- 粗密波
横波
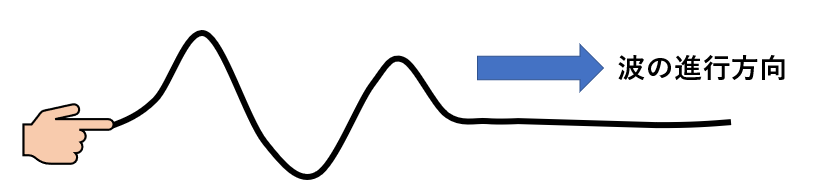
水平方向に張ったロープの端を鉛直方向に振動させると、波は水平方向に進んでいきます。
このように媒体の振動方向と波の進行方向が垂直であるような波を【横波】といいます。
横波は目で見ても波の形になっているのでわかりやすいです。
縦波
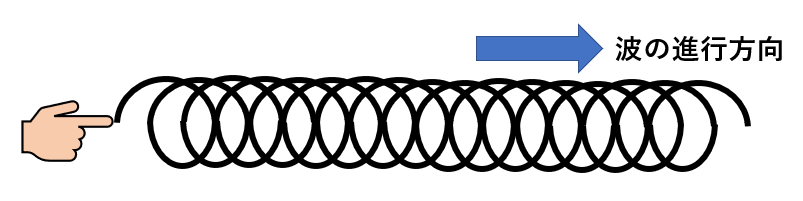
いっぽう縦波は、横波とはちがい、媒体の振動方向と波の進行方向が同じです。
縦波と横波を図解にしてみるとこんな感じ 🙂
| 縦波 | 横波 |
 |
 |
ちなみに縦波では、媒体のつまった密なところとまばらな疎な部分が交互にできるので、そのような波を【粗密波(そみつは)】ともいいます。
さらに縦波のグラフを見ていくと、以下のようになります。
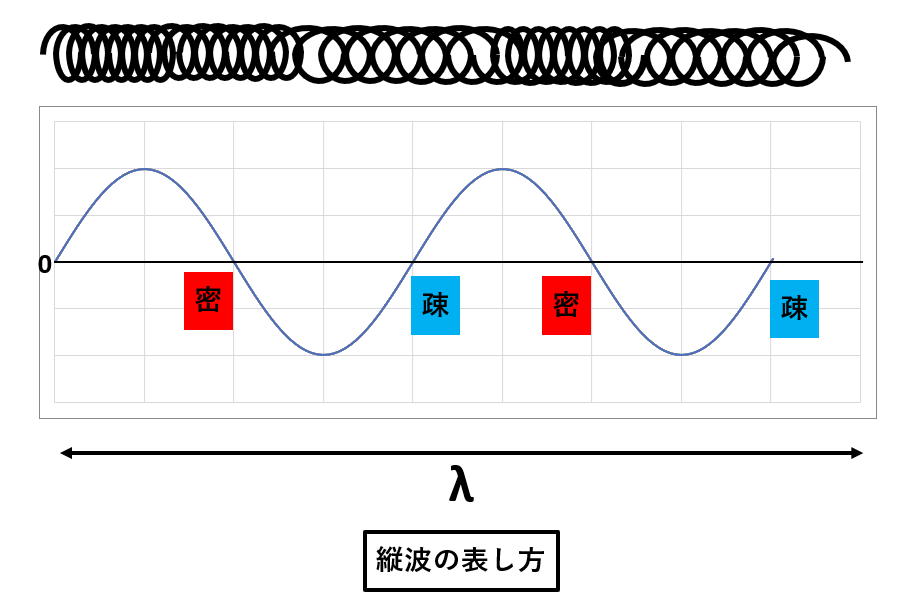
山から谷に移るところが【密】、谷から山に移るところが【疎】となります。
一方、波の干渉については、また別記事でまとめていますので、併せてご確認ください。
物理の波長グラフ②正弦波について
波の形が正弦曲線(サインカーブ)で表されるものを正弦波といいます。
以下の図のように、媒質が少しずつ遅れて単振動をすると正弦波になります。
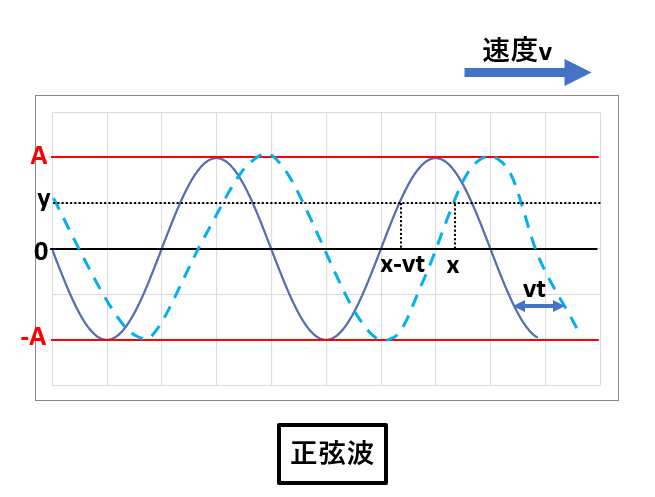
そして振幅Aの正弦波がX軸上を正の方向に速度vで進み、時刻t=0で上記の図(実線)のようになったとします。
そのときの実践の波形の式は
y=-Asin2π(x/λ)
となります。(t秒後:破線)
このときの座標xの点の媒質の変位yは、実践の波の座標x-vtにおける変位と同じです。
したがって点線の波を表す式は、実線の波の式xをx-vtに置き換えて
y=Asin2π(vt/λ-x/λ)
v/λ=f=1/Tであるから、正弦波を表す式は以下のとおりです。
y=Asin2π(t/T-x/λ)
tの違いから波はそれぞれ異なり、グラフに表すとこんな感じになります。
| 時間t | 波のグラフ |
| t=0 | 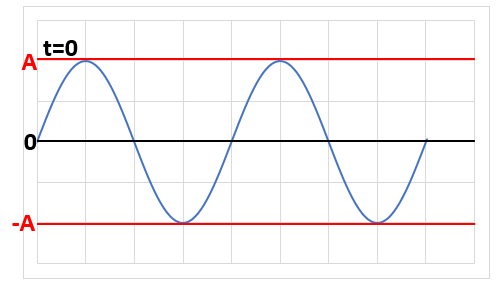 |
| t=T/4 | 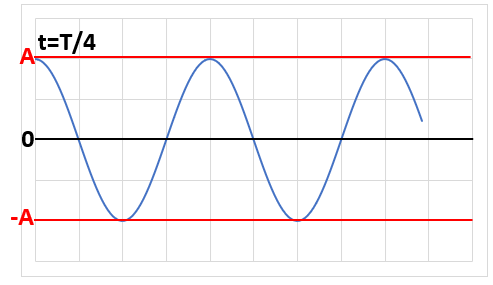 |
| t=T/2 | 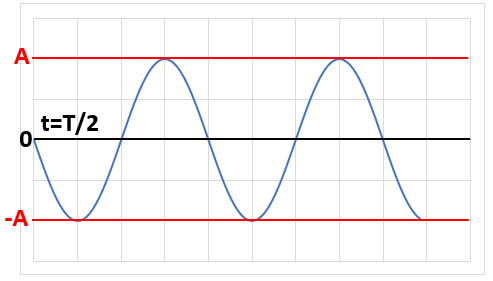 |
| t=3/4T | 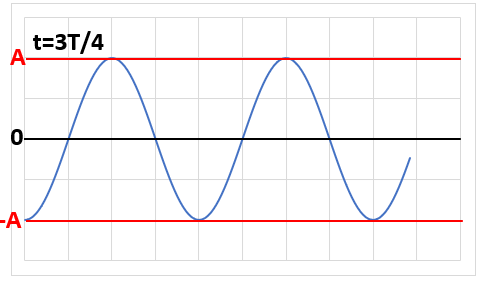 |
| t=T | 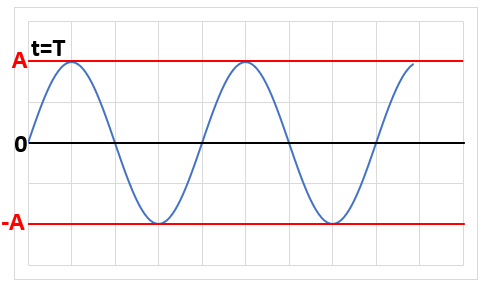 |
そしてy=Asin2π(t/T-x/λ)の角度を表す部分2π(t/T-x/λ)=Φとなり、それを位相(いそう)と呼びます。
式のtをt+Tで置き換えると、そのときの位相Φ’は、Φ’=2π(t/T-x/λ)+2πとなり、sinΦ=sinΦ’だから、波を表す関数の値はまったく同じ。
さらにxをx+λに置き換えても同じこと言えます。
つまり、時間では1周期ごとに、空間では1波長ごとに、媒質の振動の位相が同じになるというわけです。
物理の波長!振動や波の基本と公式
たとえば、池に石を投げると、水面に円形の波が広がりますよね。
このように、物質のある点に起こった運動がその物質内を伝わっていく現象を波または波動といい、波を伝える物質を媒質、振動を始めた点を波原といいます。
また、壁などにロープを水平に張り、一端を手でもちます。
手で素早く上にあげて元にもどすと、ひとつの山だけの波ができて動いていきます。
このように山または谷がひとつだけの単独の波を「パルス波」と言います。
一方で、手を連続して上下に動かすと、山と谷が交互に並んだ「連続波」ができる仕組みです。
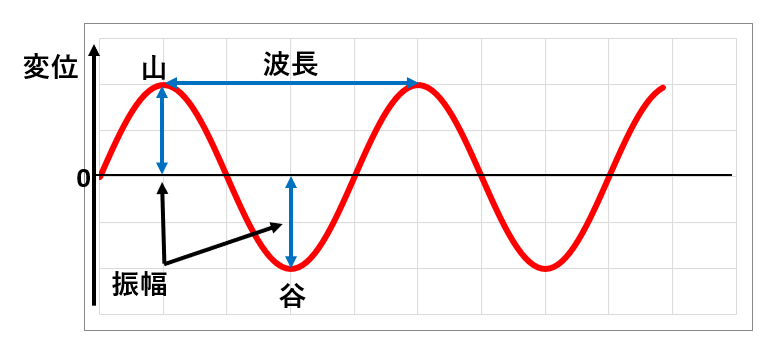
連続波は1つの山から隣の山まで、あるいは1つの谷から隣の谷までの長さが波長となります。
さらに波を表す量として、用語や公式をまとめました。
参考にしてください。
| 波長 | 波源の1回の振動によってできる波の長さ |
| 振動数 | 媒質が振動して、毎秒往復する回数のこと |
| 周期 | 媒質が1回往復するのに要する時間
振動数をf[Hz(ヘルツ)]、周期をT[s]とすると公式は以下のとおり T=1/f |
| 波の速さ | 波源の振動数がf[Hz(ヘルツ)]のとき、波は1秒間に波長λ[m]のf倍だけ前方に進む
波の速さをv[m/s]とすると、1秒間にv×1m進み、公式は以下のとおり v=fλ |
| 変位 | 波によって媒質がもとの位置から動いた(ずれた)距離 |
| 振幅 | 変位の最大値(山の高さまたは谷の深さ)のこと |
縦波と横波の違い!正弦波などグラフでわかりやすくまとめ
波の伝わり方
| 振動と波 | 周期T、振動数f、波長λ、速さvの間の関係式
T=1/f v=fλ |
  |
| 正弦波 | 波の形が正弦曲線(サインカーブ)で表されるもの
y=Asin2π(t/T-x/λ) |
.png) |
| 横波と縦波 | 横波:媒質が波の進行方向に垂直に振動する |  |
| 縦波:媒質が波の進行方向と同じ方向に振動する |  |
以上です。
ありがとうございました。