回帰分析とは？考え方や手順例をわかりやすく解説

回帰分析とは？

散布図にプロットした多くの点（2つの変数による値）を線で代表することを【回帰】と言います。

回帰とは平均に帰るという意味があるんです。

説明変数が1つの場合は単回帰、2つ以上の場合は重回帰と呼んでいます。

つまり、この近似式を導きだすための分析方法を「回帰分析」というわけですね。

単回帰分析の考え方

回帰分析には単回帰分析と重回帰分析の2つがありますが、ここでは単回帰分析の考え方について解説していきます。

回帰に関するデータの構造模型

変動xに対して、実測値yの母平均E（y₁） =μ₁が

μ₁=α+βx₁（α=常数（切片）、β=母回帰係数）

となる直線関係にあるとします。

しかし実際には、実測値y₁は必ずしも直線上にあるわけではなく、以下の図のように直線からずれてきます。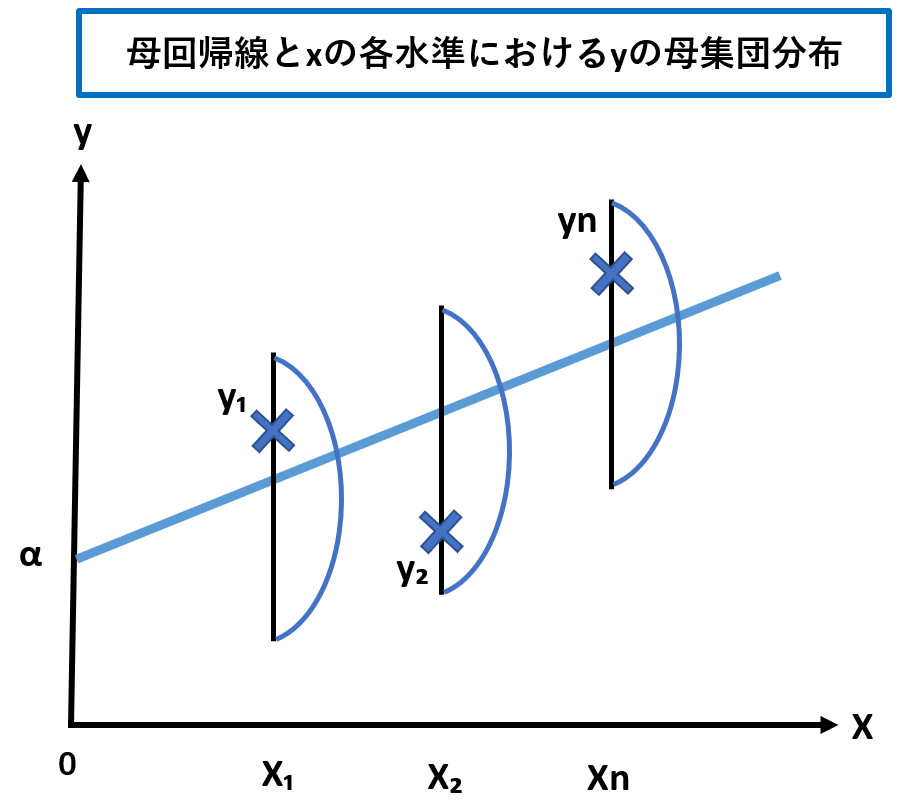

その残差変量をε₁とすると、

y₁＝α+βx₁+ε₁（α=常数（切片）、β=母回帰係数）

で表すことができます。

また、ε₁は正規母集団N（0,σ²）からお互いに独立な変量だと仮定してください。

言い換えれば、x₁の水準に関わらず、y方向のバラツキ、つまりσ²は等しく、yの母平均E（y₁）=μ₁のまわりに正規分布していると仮定したことと同じになります。

最小二乗法

α、βは未知数なので、その推定値をa、bとすれば、データ構造モデルは

y₁=a+bx₁+e₁

と表され、この時のe₁を残差といいます。

e₁=｛y₁-（a+bx₁）｝

この残差が小さいほど望ましいとされ、この残差の二乗和が最小になるようにaとbを求める方法が【最小二乗法】です。

a、bそれぞれを求めると、

a=yの平均値-b×（xの平均値）

b=Sxy/Sx（平方和Sについては次の項目で解説）

となります。

aはx=0のときのyの値で切片といい、bは回帰係数とよびます。

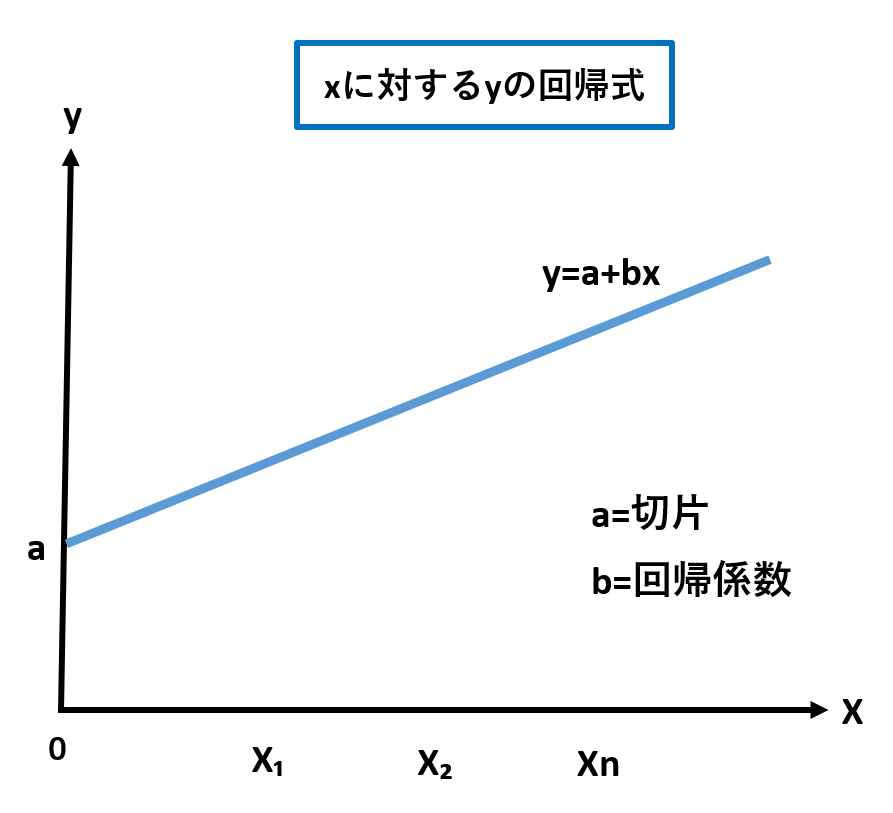
式は上記のとおり、y=a+bxとなります。

変動の分解

回帰式は、

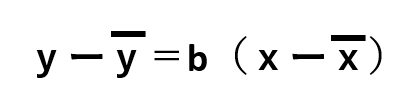
と表すこともできます。

この回帰式は、を通ります。

またデータは回帰直線のまわりにばらつくので、回帰直線により、x₁におけるy₁の母平均の推定値　は、以下の式で表します。

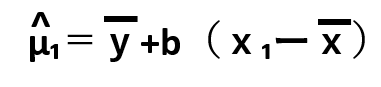
一方で、実測値は回帰線上にないので、総変動　は、次のように分解できます。

実測値による変動	St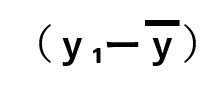
回帰による変動	Sr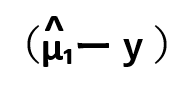
残差による変動	Se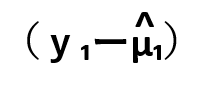

これら変動の間には、以下の関係が成り立ち、yの総変動が回帰による変動と残差変動に分解されたことを示しています。

そして上記の変動のあいだには、以下の関係式が成り立ちます。

St=Sr+Se

Sr=

b=Sxy/Sxなので、

Sr=(Sxy)²/Sx

Se=St-Sr=Sy-(Sxy)²/Sxとなります。

回帰分析（変動の分解）

よって、線型の変動を伴う場合には、変動を【回帰による変動】と【残差】とに分解することができます。

平方和を自由度で除してそれぞれの不偏分散を求め、回帰による不偏分散と残差の不偏分散とを比較し、F検定を行います。

F検定とはデータの分散が等しいかどうかを検定することだよ

そして有意であれば、直線的な関係を考えることは意味のあることだと判定し、回帰式を推定します。

単回帰分析（分散分析）の手順例

それでは、単回帰分析の手順例をみていきましょう。

ここでいう分散分析とは、説明変量xと実測値yとの間に、グラフにしたときに直線的な関係が予測された時や、回帰に意味があるかどうかの検定、検定の結果に意味があった場合、回帰係数の推定を行うものです。

例題）標本数は9組のデータで、xの平均が3.0、平方和が9.0、yの平均が7.0、平方和が5.0、xとyとの積和が6.0のとき、分散分析表を作成し、回帰に意味があるかどうかの検定と、検定結果、意味があった場合の回帰係数の推定について行いなさい。

手順①

各平方和を求めます。

まず、総変動（St）を求めると、St=Sy=5.0

次に回帰による変動Srを求めると、Sr=（Sxy）²/Sx=36/9=4

つづいて、残差による変動Seを求めると、Se=Sy-（Sxy）²/Sx=5-4=1

となります。

手順②

各自由度を求めます。(n=総データ数）

全体の自由度Φt=n-1=8

回帰による自由度Φr=1

回帰からの自由度Φe=n-2=7

手順③

各不偏分散Vと分散比F₀を求めます。

分散Vは、Vr=Sr/Φr=4/1=4

Ve=Se/Φe=1/7=0.14

よって分散比F₀は、分散比F₀=Vr/Ve≒28.6

手順④

求めた数値から、以下のような分散分析表を作成しましょう。

	平方和	自由度	不偏分散	分散比
回帰	4	1	4	F₀=28.6
残差	1	7	0.14
計	5	8

手順⑤

分散分析の結果を判定します。

ここまでで計算した分散比F₀=28.6と、F表のF（1、7：0.05）と比べてみます。（お手元のF表で確認してみてください）

F分布表は有意水準と2つの自由度（ n 1 − 1 , n 2 − 1 ）を使って、有意水準に対する統計量を計算する表

F₀=28.6>F（1、7：0.05）=5.59で、回帰による変動が残差による変動よりも総変動に与える影響が大きいので、回帰曲線は予測に役立つと言えます。

すなわち、直線的な関係を考えることは、「意味のあることだ」と判定できました。

手順⑥

手順①～⑤の結果から、回帰による変動が有意だと分かったので、最後に回帰式を推定します。

回帰式をy=a+bxとすると、

回帰係数b=Sxy/Sx=6/9≒0.67

切片a=yの平均値-b×（xの平均値）

=7-0.67×3=4.99

となり、回帰式はy=4.99+0.67xの一次関数となります。

以上です。

【関連記事】

ありがとうございました。