踏切で列車が通り過ぎるのを待っているとき、列車が目の前を通り過ぎたとたん、汽笛や列車の音が急に低くなることに気づいたことはありませんか?
または救急車の高い音が、通り過ぎた直後には低く聞こえるのは、経験したことがあるのではないでしょうか。

このように、音の波源が動くことによって、その波の振動数が大きく、あるいは小さく観測される現象を【ドップラー効果】といいます。
そんなわけで今回のテーマは【ドップラー効果】
定義や公式に加え、ドップラー効果の計算問題(例題)も合わせてわかりやすく解説していきますのでぜひチャレンジしてみてください。
それではさっそく参りましょう、ラインナップは目次からどうぞ 🙂
目次
ドップラー効果をわかりやすく!原理や計算&正負の考え方
ドップラー効果とは、音の波源が動くことによって、その波の振動数が大きくあるいは小さく観測される現象のことです。
なぜ、ドップラー効果で音が大きく聞こえたり小さく聞こえたりするのかは、音波の速度vが関係しています。
音波の速度の公式は【v=fλ】
音波の速度vは、音の振動数f[Hz]と波長λ[m]がポイントです。
たとえば、水たまり(水面)を一定の周期でたたくと、同心円のような波ができますよね。

この波の波長λはどこでも同じです。
ところが波源を一定の速度で移動させながら波をつくると、波源の前方では波長が短くなり、後方では波長が長くなります。
一方で、空気中を伝わる音波の速度はどこでも同じだから、v=fλより、振動数fと波長λは反比例することがわかります。
つまり、音源が移動すると、音源の前方では振動数が大きく、音が高く聞こえ、後方では振動数が小さく、音が低く聞こえるという原理です。
また、ドップラー効果をひも解くうえで、考えられるシチュエーションと公式を考えていきましょう。
まとめるとこんな感じです。
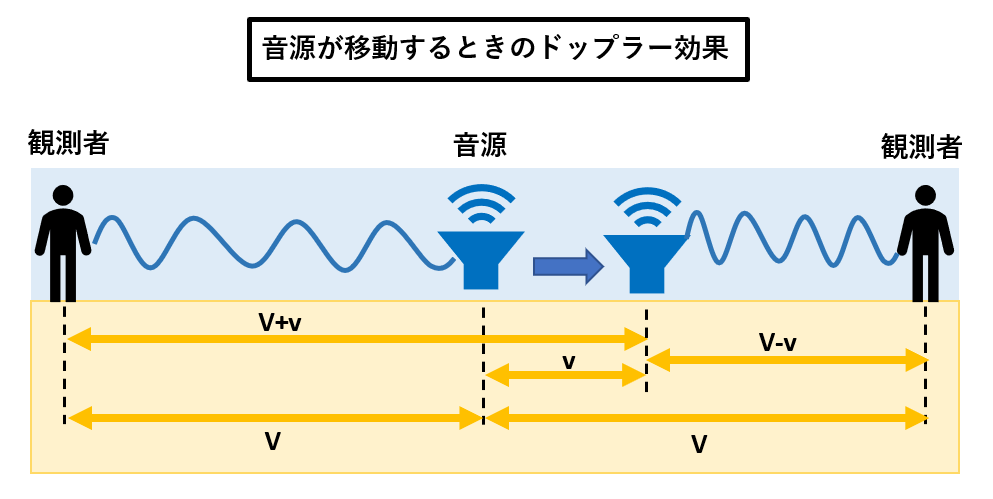
ドップラー効果をわかりやすく解説➀音源が移動する時
|
|
||
| シチュエーション | 公式 | 解説 |
| 音源が近づく場合(観測者は静止) | λ₁=(V-v)/f₀
f₁=V/λ₁=V×f₀/(V-v) |
音速をVとして、音源もvm進むから、1秒後の音源から音波の先頭の波面までの距離は(V-v)mとなる。
1秒間にはf₀個の波ができるから、音源の前方の音波の波長はλ₁=(V-v)/f₀ f₁>f₀で音は高く聞こえる |
| 音源が遠ざかる場合(観測者は静止) | λ₁’=(V+v)/f₀
f₁’=V/λ₁’=V×f₀/(V+v) |
音源の後方に送り出される音波の波長λ₂mは、(V+v)mの距離の中にf₀個の波が含まれている |
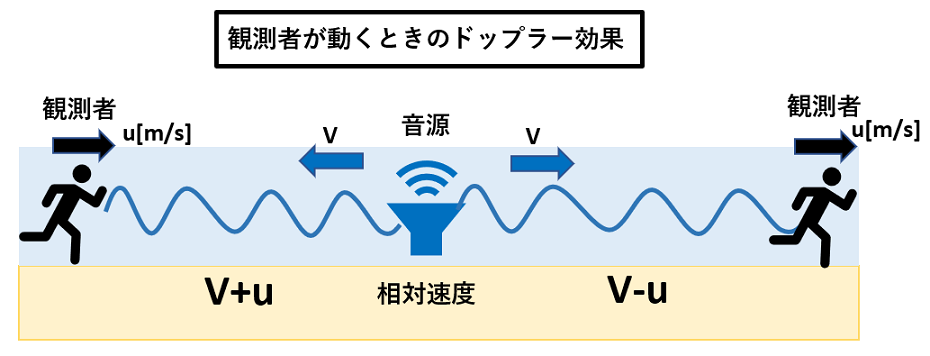
ドップラー効果をわかりやすく解説②観測者が移動する時
|
||
| シチュエーション | 公式 | 解説 |
| 観測者が遠ざかる場合 | λ₀=V/f₀
f₂=(V-u)/λ₀=(V-u)×f₀/V |
観測者が速さu[m/s]で遠ざかるとすると、観測者から見た音波の相対速度は(V-u)[m/s]となる。 |
| 観測者が近づく場合 | λ₀=V/f₀
f₂’=(V+u)/λ₀=(V+u)×f₀/V |
観測者が速さu[m/s]で近づくとすると、観測者から見た音波の相対速度は(V+u)[m/s]となる。 |
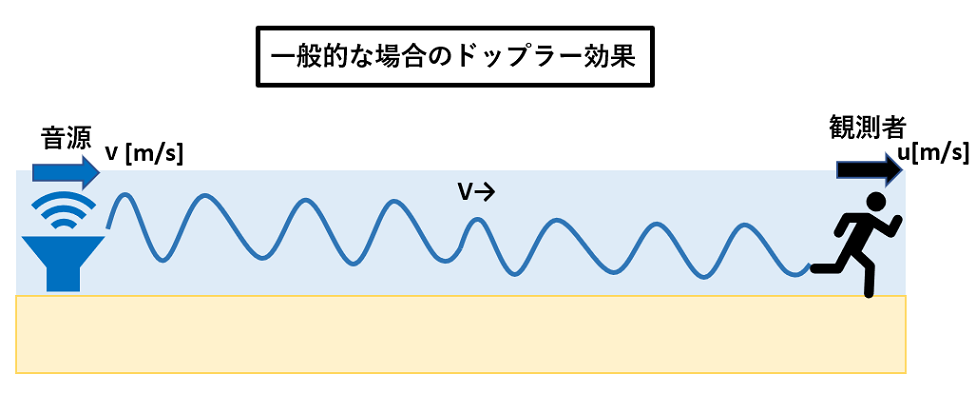
ドップラー効果をわかりやすく解説③音源も観測者も移動する時
|
||
| シチュエーション | 公式 | 解説 |
| 音源も観測者も動く場合 | λ=(V-v)/f₀
f=(V-u)/λ=(V-u)×f₀/(V-v) |
音源→観測者が正方向のとき
f[Hz]=観測される振動数、f₀[Hz]=音源の振動数 V[m/s]=音速、u[m/s]=観測者の速度、v[m/s]=音源の速度 |
遠ざかる、近づく場合を正負で考えるとよいでしょう。
また関連として、波の波長グラフについても併せてチェックしておいてください。
ドップラー効果をわかりやすく!計算問題を解いてみよう!
それではここで、ドップラー効果に関する例題を解いてみましょう。
ドップラー効果の計算例題1
音源が、静止している観測者に向かって音速の1/3の速さで近づいています。
このとき、観測者が聞く音の振動数は音源の出す音の振動数の何倍か求めなさい。
【解答】
音源は観測者に近づいています。
音源の速度の正負に注意して、ドップラー効果の式を使いましょう。
音速をVとすると、音源の速さはv=V/3です。
音源の振動数をf₀[Hz]とすると、観測者が聞く音の振動数f[Hz]は、
f=V×f₀/(V-V/3)=(3/2)f₀
よって(3/2)=1.5倍が解答となります。
解答:1.5倍
ドップラー効果の計算例題2
まっすぐな道路を、振動数940Hzの音を鳴らしながら観測者に近づいてくる自動車があります。
このとき静止した観測者は振動数980Hzの音として観測しました。
この自動車の速さを求めなさい。ただし、音速を340m/sとします。
【解答】
自動車の速さをVとすれば、以下の式が成り立ちます。
980=940×(340-0)/(340-V)
よってV=13.9m/s
解答:13.9m/s
ドップラー効果の計算例題3
直線上の道路において、静止している観測者に振動数1,360Hzの音源が速さ20m/sで近づくときに観測された音の振動数をf₁[Hz]とします。
一方、静止している振動数1,360Hzの音源に観測者が速さ20m/sで近づくときに観測された音の振動数をf₂[Hz]とします。
このとき、f₁とf₂の差(f₁-f₂)を求めなさい。ただし風はなく、音速を340m/sとします。
【解答】
人の速度と音源(波源)の速度は、音源(波源)から人への向きを正とすることに注意して、ドップラー効果の公式を適用しましょう。
f₁=f₀×(V-人の速度)/(V-音源(波源)の速度)=1,360×(340-0)/(340-20)=1,445Hz…①
f₂=f₀×(V-人の速度)/(V-音源(波源)の速度)=1,360×(340-(-20))/340-0=1,440Hz…②
よって①-②=f₁-f₂=1,445-1,440=5Hz
解答:5Hz
ドップラー効果をわかりやすく!原理や計算&正負の考え方まとめ
場面別でドップラー効果の公式は異なるので要チェック
|
|
||
| シチュエーション | 公式 | 解説 |
| 音源が近づく場合(観測者は静止) | λ₁=(V-v)/f₀
f₁=V/λ₁=V×f₀/(V-v) |
音速をVとして、音源もvm進むから、1秒後の音源から音波の先頭の波面までの距離は(V-v)mとなる。
1秒間にはf₀個の波ができるから、音源の前方の音波の波長はλ₁=(V-v)/f₀ f₁>f₀で音は高く聞こえる |
| 音源が遠ざかる場合(観測者は静止) | λ₁’=(V+v)/f₀
f₁’=V/λ₁’=V×f₀/(V+v) |
音源の後方に送り出される音波の波長λ₂mは、(V+v)mの距離の中にf₀個の波が含まれている |
 |
||
| シチュエーション | 公式 | 解説 |
| 観測者が遠ざかる場合 | λ₀=V/f₀
f₂=(V-u)/λ₀=(V-u)×f₀/V |
観測者が速さu[m/s]で遠ざかるとすると、観測者から見た音波の相対速度は(V-u)[m/s]となる。 |
| 観測者が近づく場合 | λ₀=V/f₀
f₂’=(V+u)/λ₀=(V+u)×f₀/V |
観測者が速さu[m/s]で近づくとすると、観測者から見た音波の相対速度は(V+u)[m/s]となる。 |
 |
||
| シチュエーション | 公式 | 解説 |
| 音源も観測者も動く場合 | λ=(V-v)/f₀
f=(V-u)/λ=(V-u)×f₀/(V-v) |
音源→観測者が正方向のとき
f[Hz]=観測される振動数、f₀[Hz]=音源の振動数 V[m/s]=音速、u[m/s]=観測者の速度、v[m/s]=音源の速度 |
以上です。
ありがとうございました。