
熱力学第二法則とは、熱力学において可逆過程および不可逆過程、また不可能な過程を定める法則です。
熱力学的に可能な操作から、熱力学的エントロピーの増大則が示されています。
…と言っても、よく分からないと感じる人も多いかと思うので。(笑)
受熱量やt‐s線図、逆カルノーサイクルなど、具体的な話も交えながら解説していきますね 🙂

目次
受熱量とは?求め方・公式とts線図や逆カルノーサイクルなどを解説
まず熱力学の第二法則で知っておきたいのは、
熱力学の第二法則
- 熱機関と冷凍機・ヒートポンプ
- カルノーサイクルと逆カルノーサイクル
- エントロピー
の3つです。
それぞれについてくわしくみていきましょう。
熱機関と冷凍機・ヒートポンプ
熱機関とは、温度の高い高熱源から熱を受けて使途を取り出す機械のこと。
一方、冷凍機やヒートポンプは、温度の低い低温熱源から温度の高い高温熱源へ熱をくみ上げる機械のことです。
ちなみに熱を奪う(冷凍、冷房する)ことを目的とするものは冷凍機と呼ばれ、熱を捨てる(加熱する)ことを目的にするものはヒートポンプと呼ばれています。
それぞれの熱効率や成績係数の公式はこんな感じ 🙂
| 熱機関の熱効率 | Лth=W/Q₁
=(Q₁-Q₂)/Q₁=1-Q₂/Q₁ |
Q₁:供給される熱量
Q₂:放出する熱量 W:仕事量 |
| 冷凍機の成績係数(COP) | εr=Q₂/W
=Q₂/(Q₁-Q₂) |
Q₁:放出する熱量
Q₂:供給される熱量 W:仕事量 |
| ヒートポンプの成績係数(COP) | εh=Q₁/W
=Q₁/(Q₁-Q₂) |
Q₁:放出する熱量
Q₂:供給される熱量 W:仕事量 |
これらの公式は、いずれも割合の値となり、単位はありません。
またここで注意すべきことは、冷凍機およびヒートポンプの熱量Qと仕事量Wの向きは、熱機関と逆になっているので注意してください。
さらに熱力学★第一法則についても併せて確認しておくとよいでしょう。
受熱量!カルノーサイクルと逆カルノーサイクル
.png)
等温変化と断熱変化を組み合わせ、高温熱源から熱を受け取り低温熱源に熱を排出するサイクルを【カルノーサイクル】と呼びます。
このサイクルは、受熱量をすべて仕事に変換する理想的な状態変化である等温変化を用いていることから、熱機関のなかで最も高い熱効率を有します。

一方で、カルノーサイクルを逆向きに運転し、低温熱源から熱を吸い上げ、高温熱源に放出するサイクルを【逆カルノーサイクル】と呼びます。
つまり、これらのカルノーサイクルでは、【受熱量Q₁と放熱量Q₂の比は、高温熱源の温度T(h)と低温熱源の温度T(L)の比に等しい】
と定義できるというわけです。
公式は以下の表にまとめましたので参考にしてください。
| 受熱量Q₁と放熱量Q₂の比は、高温熱源の温度T(h)と低温熱源の温度T(L)の比に等しい | Q₂/Q₁=T(h)/T(L) | Q₁:受熱量
Q₂:放熱量 T(h):高温熱源の温度 T(L):低温熱源の温度
|
| 熱機関であるカルノーサイクルの熱効率 | Лth=W/Q₁
=1-Q₂/Q₁ =1-T(h)/T(L) |
|
| 逆カルノーサイクル冷凍機の成績係数(COP) | εr=Q₂/(Q₁-Q₂)
=T(L)/(T(h)-T(L)) |
|
| 逆カルノーサイクルヒートポンプの成績係数(COP) | εh=Q₁/(Q₁-Q₂)
=T(h)/(T(h)-T(L)) |
また使用する温度は、いずれも高温熱源、低温熱源の絶対温度T(h)、T(L)【K】であることに注意してください。
エントロピー!ts線図の図解
エントロピーとは、ある2つの状態間を可逆的に変化させたとき、その変化の経路に無関係に、∫dQ/Tの値は一定であり、その値のことを指しています。
記号はSで表します。
そして状態変化の経路に無関係であることから、「エントロピーは状態のみで決まる量(状態量)」とも言えるでしょう。
また、状態1から状態2まで変化したとき、エントロピーの変化量ΔS=S₂-S₁は、
ΔS=∫₁²dQ/T(微分表現ではdS=dQ/T)
エントロピーは不可逆変化を表す量でもあり、不可逆変化が生じると、エントロピーは増加します。
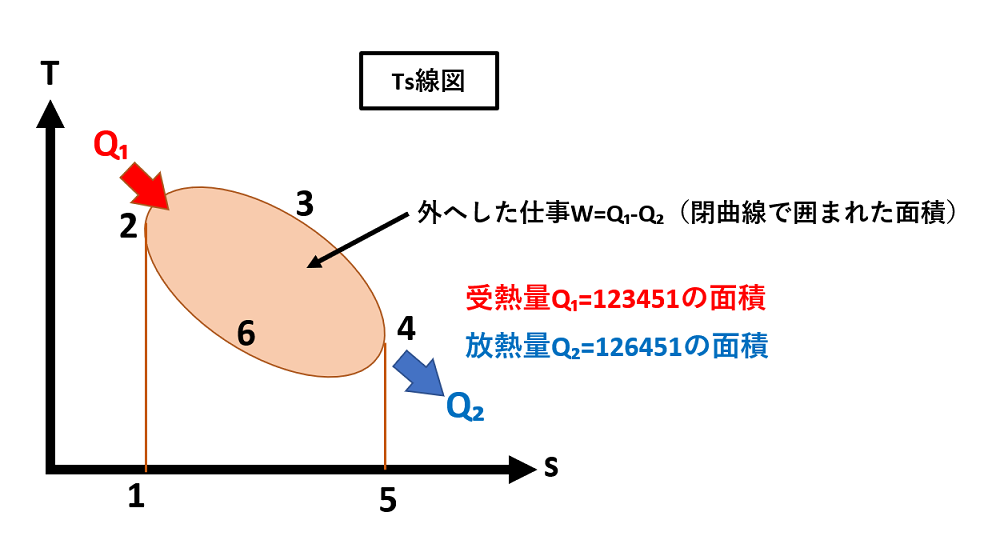
一方で、温度TとエントロピーSを両軸にとった線図をTs線図といい、pV線図とともに、サイクルの表示によく使用されます。(上記図参照)
微小な熱量dQは、エントロピー変化を用いて表すと、dQ=Tds
したがって、Q=∫Tds
すなわち、Ts線図上に表された状態変化曲線とs軸で囲まれた面積は熱量を表しています。
| エントロピー:S | ある2つの状態間を可逆的に変化させたとき、その変化の経路に無関係に、∫dQ/Tの値は一定であり、その値のことを指す |
| 状態1から状態2まで変化したときのエントロピー変化量:ΔS | ΔS=∫₁²dQ/T(微分表現ではdS=dQ/T) |
| 微小な熱量dQと熱量Q | エントロピー変化を用いて表すとdQ=Tds
Q=∫Tds |
受熱量とは?ts線図や逆カルノーサイクルの公式まとめ
受熱量は受け取る側、放熱量は出す側の熱
| 受熱量Q₁と放熱量Q₂の比は、高温熱源の温度T(h)と低温熱源の温度T(L)の比に等しい | Q₂/Q₁=T(h)/T(L) | Q₁:受熱量
Q₂:放熱量 T(h):高温熱源の温度 T(L):低温熱源の温度
|
| 熱機関であるカルノーサイクルの熱効率 | Лth=W/Q₁
=1-Q₂/Q₁ =1-T(h)/T(L) |
|
| 逆カルノーサイクル冷凍機の成績係数(COP) | εr=Q₂/(Q₁-Q₂)
=T(L)/(T(h)-T(L)) |
|
| 逆カルノーサイクルヒートポンプの成績係数(COP) | εh=Q₁/(Q₁-Q₂)
=T(h)/(T(h)-T(L)) |

| エントロピー:S | ある2つの状態間を可逆的に変化させたとき、その変化の経路に無関係に、∫dQ/Tの値は一定であり、その値のことを指す |
| 状態1から状態2まで変化したときのエントロピー変化量:ΔS | ΔS=∫₁²dQ/T(微分表現ではdS=dQ/T) |
| 微小な熱量dQと熱量Q | エントロピー変化を用いて表すとdQ=Tds
Q=∫Tds |
以上です。
ありがとうございました。
